浙江省台州市椒江区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-03 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 下列各式中,为最简二次根式的是( )A、 B、 C、 D、2. 在一次排球垫球测试后,随机抽取八年级(2)班的5名同学的成绩(单位:个)如下:38.40.40,42,45,这组数据的众数是( )A、38 B、40 C、41 D、423. 下列四组线段中,可以构成直角三角形的是( )A、1、2、3 B、2、3、4 C、3、4、5 D、5、6、74. 要使代数式 有意义,则x的取值范围是( )A、x> B、x< C、x≥ D、x≤5. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沼作对折,使得点B落在边AD上的点B处,折痕与边BC交于点E,则CE的长为( )
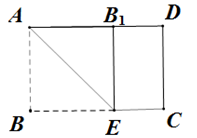 A、2cm B、3cm C、4cm D、6cm6. 如图是一种古代计时器—“漏壶”的示意图,壶内盛有一定量的水,水从壶下的小孔漏出,壶壁上面有刻度,人们可以根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度.下列图象适合表示y与x的函数关系的是(不考虑水量变化对压力的影响) ( )
A、2cm B、3cm C、4cm D、6cm6. 如图是一种古代计时器—“漏壶”的示意图,壶内盛有一定量的水,水从壶下的小孔漏出,壶壁上面有刻度,人们可以根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度.下列图象适合表示y与x的函数关系的是(不考虑水量变化对压力的影响) ( ) A、
A、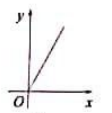 B、
B、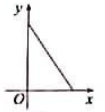 C、
C、 D、
D、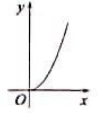 7. 关于函数y=-x+1的图象与性质,下列说法错误的是( )A、图象不经过第三象限 B、图象是与y=-x-1平行的一条直线 C、y随x的增大而减小 D、当-2≤x≤1时,函数值y有最小值38. 为了在甲、乙两名运动员中选拔一人发加全省射击比赛,对他们的射击水平进行考核.在相同的情况下,两人的比赛成绩经统计计算后如下表;
7. 关于函数y=-x+1的图象与性质,下列说法错误的是( )A、图象不经过第三象限 B、图象是与y=-x-1平行的一条直线 C、y随x的增大而减小 D、当-2≤x≤1时,函数值y有最小值38. 为了在甲、乙两名运动员中选拔一人发加全省射击比赛,对他们的射击水平进行考核.在相同的情况下,两人的比赛成绩经统计计算后如下表;运动员
射击次数
中位数(环)
方差
平均数(环)
甲
15
7
1.6
8
乙
15
8
0.7
8
某同学根据上表分析得出如下结论:①甲、乙两名运动员成绩的平均水平相同;②乙运动员优秀的次数多于甲运动员(环数≥8环为优秀);③甲运动员成绩的波动比乙大,上述结论正确的是( )
A、①②③ B、①② C、①③ D、②③9. 如图,在菱形ABCD中,点E,F、G,H分别是边,AB,BC,CD和DA的中点,连接EF.FG.GH和HE.若EH=3EF,则下列结论正确的是( )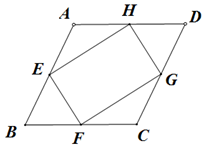 A、AB= EF B、AB=2 EF C、AB=3EF D、AB= EF10. 在平面直角坐标系中,定义:已知图形W和直线l,如果图形W上存在一点Q,使得点Q到直线1的距离小于或等于k,则称图形W与直线1“k关联”.已知线段AB,其中点A(1,1),B(3.1).若线段AB与直线y=-x+b“ 关联”,则b的取值范围是( )A、-1≤b≤ B、0≤b≤4 C、0≤b≤6 D、 ≤b≤6
A、AB= EF B、AB=2 EF C、AB=3EF D、AB= EF10. 在平面直角坐标系中,定义:已知图形W和直线l,如果图形W上存在一点Q,使得点Q到直线1的距离小于或等于k,则称图形W与直线1“k关联”.已知线段AB,其中点A(1,1),B(3.1).若线段AB与直线y=-x+b“ 关联”,则b的取值范围是( )A、-1≤b≤ B、0≤b≤4 C、0≤b≤6 D、 ≤b≤6二、填空题(本题有6小题,每小题3分,共18分)
-
11. = .12. 直线y=3x向下平移3个单位长度得到的直线是13. 某招聘考试分笔试和面试两种,小明笔试成绩90分,面试成绩85分,如果笔试成绩、面试成绩按3:2计算,那么小明的平均成绩是分
14. 如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,若AB=5,AD=3,则BD的长为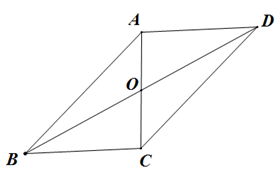 15. 小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间r(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是_分钟.
15. 小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间r(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是_分钟. 16. 如图,在正方形ABCD中,点E是边CD上一点,BF⊥AE,垂足为F,将正方形沿AE.BF切割分成三块,再将△ABF和△ADE分别平移,拼成矩形BGHF.若BG=kBF,则 (用含k的式子表示)
16. 如图,在正方形ABCD中,点E是边CD上一点,BF⊥AE,垂足为F,将正方形沿AE.BF切割分成三块,再将△ABF和△ADE分别平移,拼成矩形BGHF.若BG=kBF,则 (用含k的式子表示)

三、解答题(本题有8小题,第17题6分,第18~19题每题5分,第20-22题每题6分, 第23题8分,第24题10分,共52分
-
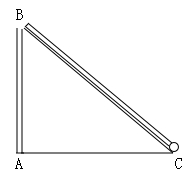
17. 计算:(1)、(2)、( +3)( -5)18. 如图,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处.木杆折断之前有多高?
 19. 如图,在6x6的网格中,点A,B在格点(小正方形的顶点)上.试在各网格中画出顶
19. 如图,在6x6的网格中,点A,B在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,且符合相应条件的图形.
 (1)、在图1中画一个以AB为边的平行四边形;(2)、在图2中画一个以AB为对角线的正方形.20. 已知一次函数y=kx+b的图象经过点A(0,2)和点B(1.3).(1)、求此一次函数的解析式;(2)、若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.21. 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
(1)、在图1中画一个以AB为边的平行四边形;(2)、在图2中画一个以AB为对角线的正方形.20. 已知一次函数y=kx+b的图象经过点A(0,2)和点B(1.3).(1)、求此一次函数的解析式;(2)、若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.21. 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2
(1)、求这15位营销人员该月销售量的平均数、中位数和众数:(2)、假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由,22. 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边三角形ABD,点E是线段AD的中点,连接CE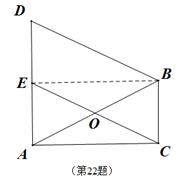 (1)、求证:四边形BDEC为平行四边形;(2)、若AB=8,求四边形BDEC的面积,23. 在“美丽中国,清洁乡村”活动中,李家村提出两种购买垃圾桶方案:方案1:不分类垃圾桶免费赠送,以后每月的垃圾处理费用800元:方案2:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用200元;设方案1的总费用为y1元,方案2的总费用为y2元,交费时间为x个月.
(1)、求证:四边形BDEC为平行四边形;(2)、若AB=8,求四边形BDEC的面积,23. 在“美丽中国,清洁乡村”活动中,李家村提出两种购买垃圾桶方案:方案1:不分类垃圾桶免费赠送,以后每月的垃圾处理费用800元:方案2:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用200元;设方案1的总费用为y1元,方案2的总费用为y2元,交费时间为x个月.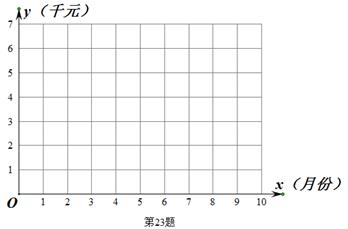 (1)、分别写出y1 , y2与x的函数关系式(2)、在同一坐标系内,画出函数y1 , y2的图象;(3)、在不考虑垃圾桶使用寿命的情况下,哪种方案省钱?24. 如图1,在菱形ABCD中,∠B=60°,把一个含60°角的直角三角板和这个菱形摆放在一起,使三角板60°角的顶点和菱形的顶点A重合,60°角的两边分别与菱形的边BC,CD交于点E,F.
(1)、分别写出y1 , y2与x的函数关系式(2)、在同一坐标系内,画出函数y1 , y2的图象;(3)、在不考虑垃圾桶使用寿命的情况下,哪种方案省钱?24. 如图1,在菱形ABCD中,∠B=60°,把一个含60°角的直角三角板和这个菱形摆放在一起,使三角板60°角的顶点和菱形的顶点A重合,60°角的两边分别与菱形的边BC,CD交于点E,F.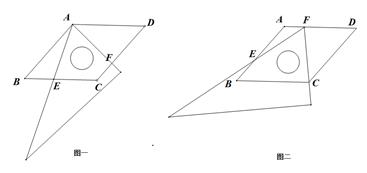 (1)、线段BE,DF与AB三者之间的数量关系为;(2)、请证明(1)中的结论:(3)、如图2,变换三角板的位置,使60°角的顶点F在边AD上,60°角的其中一边经过点C,另一边与边AB交于点E,那么(1)中得到的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
(1)、线段BE,DF与AB三者之间的数量关系为;(2)、请证明(1)中的结论:(3)、如图2,变换三角板的位置,使60°角的顶点F在边AD上,60°角的其中一边经过点C,另一边与边AB交于点E,那么(1)中得到的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.