浙江省湖州市吴兴区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-03 类型:期末考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 计算a•a2的结果是( )A、a2 B、a3 C、2a3 D、a2. 如图,∠1和∠2是同位角的是( )A、
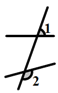 B、
B、 C、
C、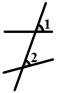 D、
D、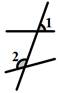 3. 计算的值是( )A、 B、 C、 D、4. 下列调查中,适宜采用全面调查的是( )A、对全国初中生手机使用情况的调查。 B、疫情防控期间,对某小区人员有无去往武汉的调查。 C、对全市初一学生使用钉钉上网课满意率的调查。 D、对全省初一学生作业量的调查。5. 下列各组数中,是二元一次方程2x﹣3y=5的解的是( )A、 B、 C、 D、6. 分式 可变形为( )A、 B、 C、 D、7. 已知把一个把多项式分解因式,得结果(x+1)(x﹣3),则这个多项式是( )A、x2+3x-2 B、x2+2x-3 C、x2-2x-3 D、x2-3x+28. 长为a , 宽为b的长方形,它的周长为10,面积为5,则a2b+ab2的值为( )A、25 B、50 C、75 D、1009. 将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n , 则下列结论中一定正确的是( )
3. 计算的值是( )A、 B、 C、 D、4. 下列调查中,适宜采用全面调查的是( )A、对全国初中生手机使用情况的调查。 B、疫情防控期间,对某小区人员有无去往武汉的调查。 C、对全市初一学生使用钉钉上网课满意率的调查。 D、对全省初一学生作业量的调查。5. 下列各组数中,是二元一次方程2x﹣3y=5的解的是( )A、 B、 C、 D、6. 分式 可变形为( )A、 B、 C、 D、7. 已知把一个把多项式分解因式,得结果(x+1)(x﹣3),则这个多项式是( )A、x2+3x-2 B、x2+2x-3 C、x2-2x-3 D、x2-3x+28. 长为a , 宽为b的长方形,它的周长为10,面积为5,则a2b+ab2的值为( )A、25 B、50 C、75 D、1009. 将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n , 则下列结论中一定正确的是( )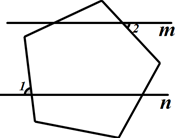 A、∠1=∠2+36° B、∠1=∠2+72° C、∠1+∠2=90° D、2∠1+∠2=180°10. 如图,为了美化校园,某校要在面积为60平方米长方形空地ABCD中划出长方形EBKR和长方形QFSD , 若两者的重合部分GFHR恰好是一个边长为3米的正方形,现将图中阴影部分区域作为花圃,若长方形空地ABCD的长和宽分别为m和n , m>n , 花圃区域AEGQ和HKCS总周长为20米,则m-n的值为( )
A、∠1=∠2+36° B、∠1=∠2+72° C、∠1+∠2=90° D、2∠1+∠2=180°10. 如图,为了美化校园,某校要在面积为60平方米长方形空地ABCD中划出长方形EBKR和长方形QFSD , 若两者的重合部分GFHR恰好是一个边长为3米的正方形,现将图中阴影部分区域作为花圃,若长方形空地ABCD的长和宽分别为m和n , m>n , 花圃区域AEGQ和HKCS总周长为20米,则m-n的值为( )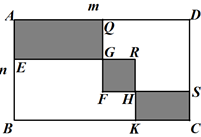 A、4米 B、3米 C、2米 D、2.5米
A、4米 B、3米 C、2米 D、2.5米二、填空题(共6小题,每小题4分,共24分)
-
11. 将0.00025用科学记数法表示 .12. 若分式 有意义,则x的取值范围是 .13. 为了解某校学生对篮球、足球、网球、乒乓球、羽毛球这五种球类运动的喜爱程度,小王进行了抽样调查.在绘制扇形统计图时,由于时间仓促,部分信息还没有绘制完成,结果如图所示.根据图中的信息,这批被抽样调查的学生最喜欢乒乓球的人数与最喜欢网球的人数和是 .
 14. 已知分式方程 无解,则a= .15. 对于两个非零实数x、y , 定义一种新运算 , 若 ,则 的值是 .16. 2020年6月1日,湖州市政府发布了全新湖州城市形象标识,小周同学对新的形象标识很感兴趣,用电脑绘画软件绘制了如下图形,其中第(1)个图形有3个形象标识,第(2)个图形有7个形象标识,第(3)个图形有13个形象标识,按此规律绘制下去。
14. 已知分式方程 无解,则a= .15. 对于两个非零实数x、y , 定义一种新运算 , 若 ,则 的值是 .16. 2020年6月1日,湖州市政府发布了全新湖州城市形象标识,小周同学对新的形象标识很感兴趣,用电脑绘画软件绘制了如下图形,其中第(1)个图形有3个形象标识,第(2)个图形有7个形象标识,第(3)个图形有13个形象标识,按此规律绘制下去。
……
………
(1)、小周绘制的第(5)个图形中有个形象标识.(2)、小周绘制的第(n)个图形中有个形象标识.三、简答题(共8小题,共66分)
-
17. 化简(a+3)2 -(a﹣3)(a+3)18.(1)、解二元一次方程组 ;(2)、解分式方程 .19. 如图,已知∠ABC+∠C=180°,∠CBD=75°,BD平分∠ABC , 求∠D的度数。
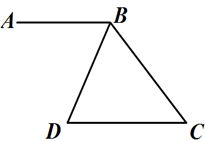 20. 先化简,再求值 ,其中x=3。21. “品中华诗词,寻文化基因”。为深入推进传统文化教育,某校举办了“中华诗词大赛”,从七年级600名学生中随机抽取部分学生组成一班进行成绩登记。小陆同学根据老师的成绩登记表绘制了如下不完整的频数表。
20. 先化简,再求值 ,其中x=3。21. “品中华诗词,寻文化基因”。为深入推进传统文化教育,某校举办了“中华诗词大赛”,从七年级600名学生中随机抽取部分学生组成一班进行成绩登记。小陆同学根据老师的成绩登记表绘制了如下不完整的频数表。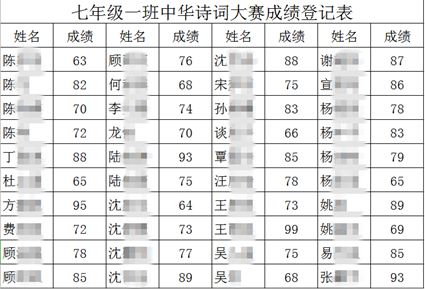
七年级一班中华诗词大赛成绩频数表
组别
成绩x(分)
人数
百分比
A
60≤x<70
8
20%
B
70≤x<80
a
m%
C
80≤x<90
b
n%
D
90≤x≤100
4
10%
请观察图表,解答下列问题:
(1)、频数表中a= , b= , m= , n= , .(2)、若按照频数表中的组别,将七年级一班中华诗词大赛的成绩绘制成扇形统计图,则组别A所对应的圆心角度数是 .(3)、如果成绩达到80分及以上的同学为优秀,请估计该校七年级600名学生中成绩优秀的人数。22. 2020年由于新冠肺炎爆发,为预防疫情专家提出了“勤洗手,戴口罩” 的措施,口罩在市场上供不应求,生产口罩的主要材料是熔喷布。已知1吨熔喷布可以生产105万只医用一次性口罩,或者60万只KN95口罩。某生产熔喷布的企业要求在规定时间内完成100吨熔喷布的订单,为提高产量,现对生产车间进行改造,改造后每天比改造前多生产4吨熔喷布,结果在规定时间内多生产了40吨熔喷布。(1)、现有一批熔喷布,若全部用来生产医用一次性口罩则可以生产420万只,则这批熔喷布全部用来生产KN95口罩则可以生产万只;(2)、求该企业改造后熔喷布的日产量和企业要求规定的天数。23. 如图,现有一块含有30°的直角三角板ABC , 且l1∥l2 , 其中∠ABC=30°。 (1)、如图(1),当直线l1 和l2分别过三角板ABC的两个顶点时,且∠1=35°,则∠2=°(2)、如图(2),当∠ADE=80°时,求∠GFB的度数。(3)、如图(3),点Q是线段CD上的一点,当∠QFC=2∠CFN时,请判断∠ADE和∠QFG的数量关系,并说出理由。24. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。
(1)、如图(1),当直线l1 和l2分别过三角板ABC的两个顶点时,且∠1=35°,则∠2=°(2)、如图(2),当∠ADE=80°时,求∠GFB的度数。(3)、如图(3),点Q是线段CD上的一点,当∠QFC=2∠CFN时,请判断∠ADE和∠QFG的数量关系,并说出理由。24. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。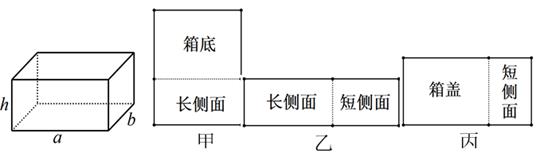 (1)、填空:用含a、b、h的代数式表示以下面积:
(1)、填空:用含a、b、h的代数式表示以下面积:甲的面积;乙的面积;丙的面积.
(2)、当h=20cm时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;(3)、现将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型(如图②),且这样的圆柱体模型的高刚好与木箱的高相等。问:一个上述长方体木箱中最多可以放个这样的圆柱体模型。