浙江省湖州市吴兴区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-03 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 以下四个商标中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列等式中，成立的是（）

A、 ${(\sqrt{5})}^{2} = 5$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ D、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$

查看试题解析
3. 若一个多边形的内角和等于1800度，则这个多边形是（）

A、十二边形 B、十边形 C、九边形 D、八边形

查看试题解析
4. 对甲、乙、丙、丁四名选手进行射击测试，每人射击10次，平均成绩均为9.5环，且他们的方差如下表所示：

选手

甲

乙

丙

丁

方差

1.56

0.60

2.50

0.40

则在这四个选手中，成绩最稳定的是（）

A、甲 B、乙 C、丙. D、丁

查看试题解析
5. 受新冠肺炎疫情影响，某企业生产总值从1月份的300万元，连续两个月降至260万元，设每月平均下降率为x，则可列方程（）

A、 $300 {(1 + x)}^{2} = 260$ B、 $300 (1 - x^{2}) = 260$ C、 $300 (1 - 2 x) = 260$ D、 $300 {(1 - x)}^{2} = 260$

查看试题解析
6. 在四边形ABCD中，AB∥CD，再添加下列其中一个条件后，四边形ABCD不一定是平行四边形的是（）

A、AB＝CD B、AD＝BC C、AD∥BC D、∠A＝∠C

查看试题解析
7. 若点A（﹣3， $y_{1}$ ），B（﹣2， $y_{2}$ ），C（1， $y_{3}$ ）都在反比例函数 $y = - \frac{3}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
8. 如图，DE，NM分别是△ABC，△ADE的中位线，NM的延长线交BC于点F，则S_△_DMN：S_四边形_MFCE等于（）

A、1：5 B、1：4 C、2：5 D、2：7

查看试题解析
9. 如图，菱形纸片ABCD的边长为a，∠ABC=60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上一点P，若 $A E = 2 B E$ ，则六边形AEFCHG面积的是（）

A、 $\frac{\sqrt{3}}{3} a^{2}$ B、 $\frac{5 \sqrt{3}}{12} a^{2}$ C、 $\frac{13 \sqrt{3}}{36} a^{2}$ D、 $\frac{19 \sqrt{3}}{48} a^{2}$

查看试题解析
10. 如图，已知直线 $l_{1}$ 、 $l_{2}$ 经过坐标原点O，且 $l_{1}$ 与x轴所夹锐角为15°， $l_{2}$ 与y轴所夹锐角为30°.在直线 $l_{1}$ 和 $l_{2}$ 之间依次构造正方形 $A_{1} B_{1} C_{1} A_{2}$ 、正方形 $A_{2} B_{2} C_{2} A_{3}$ 、正方形 $A_{3} B_{3} C_{3} A_{4}$ 、正方形 $A_{4} B_{4} C_{4} A_{5}$ ……点 $A_{1}$ 、点 $A_{2}$ 、点 $A_{3}$ 、点 $A_{4}$ 、点 $A_{5}$ …依次落在直线 $l_{1}$ 上，点 $B_{1}$ 、点 $B_{2}$ 、点 $B_{3}$ 、点 $B_{4}$ …依次落在直线 $l_{2}$ 上，且 $A_{1} B_{1} = 1$ ，则点 $B_{2020}$ 的坐标为（）

A、 $(2^{2018} \sqrt{2} ， 2^{2018} \sqrt{6})$ B、 $(2^{2017} \sqrt{2} ， 2^{2017} \sqrt{6})$ C、 $(2^{2018} \sqrt{2} ， 2^{2018} \sqrt{3})$ D、 $(2^{2018} ， 2^{2018} \sqrt{3})$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 代数式 $\sqrt{x + 8}$ 有意义时，x应满足的条件是．

查看试题解析
12. 已知一组数据5，4，x，3，9的平均数为5，则x的值是。

查看试题解析
13. 已知x=1是关于方程x²+mx﹣3＝0的一个根，则m＝．

查看试题解析
14. 已知反比例函数 $y = \frac{6}{x}$ ，当 $y < 2$ 时，x的取值范围是．

查看试题解析
15. 如图，在平面直角坐标系中，点O为坐标原点，等边△ABO的边OB和菱形CDEO的边EO均在x轴上，点C在AO上， $S_{Δ A B D} = 4 \sqrt{3}$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图像经过A点，则k的值为．

查看试题解析
16. 在矩形ABCD中，AB＝2，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点B的对应点为点F．

(1)、若点F恰好落在AD边上，则AD＝．

(2)、延长AF交直线CD于点P，若PD= $\frac{1}{2}$ CD，则AD的值为．

查看试题解析

三、简答题（本题有8小题，共66分）

17. 二次根式计算

(1)、 $2 \sqrt{3} + (\sqrt{\frac{1}{3}} - \sqrt{27})$

(2)、 ${(1 - \sqrt{2})}^{2} + \sqrt{16} \div \sqrt{2}$

查看试题解析
18. 解下列一元二次方程

(1)、 $x^{2} - 25 = 0$

(2)、 $x^{2} - 4 x - 5 = 0$

查看试题解析
19. 如图，在5×5的方格纸中，每个小正方形的边长为1个单位长度，△ABC的顶点都在格点上。请回答下列问题：

(1)、求AC的长；

(2)、在图中找一格点D，使得A，B，C，D四点构成的四边形是平行四边形。

查看试题解析
20. 如图，在矩形ABCD中，过对角线BD的中点O作垂线EF，与边AD，BC分别交于点E，F，连接BE，DF。

(1)、求证：四边形EBFD是菱形；

(2)、若AD=8，AB=4，求四边形EBFD的周长。

查看试题解析

21. 在推进湖州市新冠疫情防控活动中，某社区为了了解居民掌握新冠防控知识的情况进行调查．其中A、B两小区分别有500名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息：

【信息一】A小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）：

【信息二】上图中，从左往右第四组的成绩如下：

75	75	76	76	76	76	80	80
81	82	82	83	83	84	84	84

【信息三】A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率（80分及以上为优秀）、方差等数据如下（部分空缺）：

小区	平均数	中位数	众数	优秀率	方差
A	75.1		76		277
B	75.1	77	76	45%	211

根据以上信息，回答下列问题：

(1)、求A小区从左往右第四组居民成绩的中位数，以及A小区50名居民成绩的中位数．

(2)、请估计A小区500名居民成绩达到优秀的人数．

(3)、请选择2个合适的统计量，分析A，B哪个小区的居民对新冠防控知识掌握得更好．

查看试题解析

22. 如图，一轮船以40km/h的速度由西向东航行，在途中点C处接到台风警报，台风中心点B正以20km/h的速度由南向北移动．已知距台风中心200km的区域（包括边界）都属于受台风影响区．当轮船接到台风警报时，测得BC＝500km，BA＝300km．（假定轮船不改变航向）．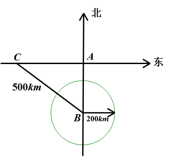

(1)、如果这艘轮船不改变航向，经过11小时，轮船与台风中心相距多远？此时，轮船是否受到台风影响？

(2)、如果这艘轮船受到台风影响，请求出轮船受到台风影响一共经历了多少小时？

查看试题解析
23. 已知，在等腰直角三角形ABC中BA=AC，∠BAC=90°，点D为BC边上一动点，点E，F分别为AB、BC边上的动点，且BE=AF

(1)、如图1，当点D为BC中点时，试说明DE和DF的关系，并说明理由；

(2)、在（1）的条件下，如图2，当点E为AB中点时，判断四边形AEDF的形状，并说明理由；

(3)、如图3，过点A作BC的平行线，交DF的延长线于点G，且满足AG=BC=4.若D点从B点出发，以1个单位长度每秒的速度向终点C运动，连结AD.设点D的运动时间为t秒（ $0 \leq t \leq 4$ ），在点D的运动过程中，图中能否出现全等三角形？若能，请直接写出整数t的值和对应全等三角形的对数；若不能，请说明理由.

查看试题解析
24. 已知反比例函数 $y_{1} = \frac{m}{x} (m > 0 ， x > 0)$ 和 $y_{2} = - \frac{m}{2 x} (x < 0)$ ，过点P（0，1）作x轴的平行线l与函数 $y_{1} ， y_{2}$ 的图象相交于点B，C.

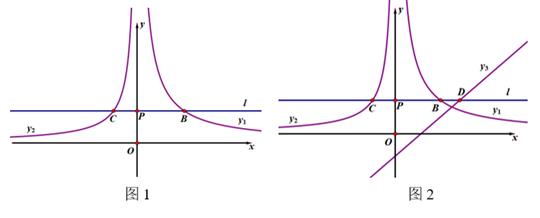(1)、如图1，若 $m = 6$ 时，求点B，C的坐标；

(2)、如图2，一次函数 $y_{3} = k x - \frac{m}{2}$ 交l于点D．
①若k＝5，B、C、D三点恰好满足其中一点为另外两点连线的中点，求m的值；

②过点B作y轴的平行线与函数y₃的图象相交于点E．当m值取不大于 $\frac{2}{3}$ 的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．

查看试题解析

选手	甲	乙	丙	丁
方差	1.56	0.60	2.50	0.40