湖北省襄阳市襄州区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-03 类型：期末考试

进入出卷网下载

一、填空题（本大题共10小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项符合题目要求，请你认为正确的选项号写在答题卡中对应位置.

1. 4的平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
2. 点 $M (5 ， - 3)$ 在第 $($ $)$ 象限．

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，AB∥CD，∠B=65°，则∠1的度数是（）

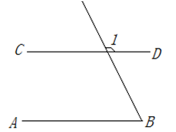A、65° B、115° C、125° D、135°

查看试题解析
4. 如图，A点的位置可以用坐标（0，－1）表示，则点C位置的坐标可以表示为（）

A、（－1，－3） B、（－3，－3） C、（－2，－2） D、（2，－2）

查看试题解析
5. 解为 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 的方程组是 ( ）

A、 ${\begin{matrix} x - y = 1 \\ 3 x + y = 5 \end{matrix}$ B、 ${\begin{matrix} x - y = - 1 \\ 3 x + y = - 5 \end{matrix}$ C、 ${\begin{matrix} x - 2 y = - 3 \\ 3 x + y = 5 \end{matrix}$ D、 ${\begin{matrix} x - y = 3 \\ 3 x - y = 1 \end{matrix}$

查看试题解析
6. 若m＞n，则下列不等式正确的是（）

A、m－4＜n－4 B、 $\frac{m}{4} > \frac{n}{4}$ C、 4m＜4n D、－2m＞－2n

查看试题解析
7. 下列调查中，调查方式选择合理的是（）

A、为了调查我市二汽生产的东风日产轿车的抗撞击能力，选择全面调查 B、为了了解我市中学生每周网课学习所用的时间，选择全面调查 C、为了了解我市唐城景区的每天的游客客流量，选择抽样调查 D、为了保证长征运载火箭的成功发射，对其所有的零部件采用抽样调查

查看试题解析
8. 某班级的一次数学考试成绩统计图如图，则下列说法错误的是（）

A、该班的总人数为40 B、得分及格 $(\geq 60$ 分 $)$ 的有12人 C、得分在 $70 ～ 80$ 分的人数最多 D、人数最少的得分段的频数为2

查看试题解析
9. 《九章算术》是中国古代第一部数学专著，它的出现标志着中国古代数学形成了完整的体系，在其方程章中有一道题：“今有五雀，六燕，集称之衡，雀俱重，燕俱轻．一雀一燕交而处，衡适平．并燕雀重一斤．问燕雀一枚各重几何？”其大意是：“现在有5只雀，6只燕，分别集中放在天平上称重，聚在一起的雀重燕轻．将一只雀一只燕交换位置而放，重量相等.5只雀、6只燕重量共一斤，问雀和燕各重多少？”古代记1斤为16两，则设1只雀x两，一只燕y两，可列出方程（）

A、 ${\begin{matrix} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{matrix}$ B、 ${\begin{matrix} 5 x + 6 y = 16 \\ 5 x = 6 y \end{matrix}$ C、 ${\begin{matrix} 5 x + 6 y = 10 \\ 4 x + y = 5 y + x \end{matrix}$ D、 ${\begin{matrix} 5 x + 6 y = 10 \\ 5 x = 6 y \end{matrix}$

查看试题解析
10. 若 $a^{2}$ =16， $| b | = 3$ ，则 $a + b$ 所有可能的值为（）

A、7 B、7或1 C、7或－1 D、±7或±1

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 计算： $| - 2 | + \sqrt[3]{- 8}$ =.

查看试题解析
12. 小华将平面直角坐标系中的小船图案向上平移了2个单位，又向左平移了3个单位，平移前小船船头A点的坐标为（1，－1），则平移后小船船头A点坐标为.

查看试题解析
13. 不等式组 ${\begin{cases} \frac{x + 1}{3} \leq 1 ， \\ x + 2 > 1 \end{cases}$ 的最小整数解为.

查看试题解析
14. 如图， $A B / / C D$ ，OM平分 $∠ B O F$ ， $∠ 2 = 55^{\circ}$ ，则 $∠ 1 =$ 度 $.$

查看试题解析
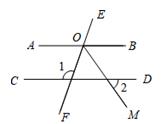15. 若关于x、y的二元一次方程组 ${\begin{matrix} x + y = 3 k \\ x - y = 5 k \end{matrix}$ 的解是二元一次方程的2x+3y=15的解，则k的值为.

查看试题解析
16. 如图，AD∥BC，∠ADC=120°，∠BAD=3∠CAD，E为AC上一点，且∠ABE=2∠CBE，在直线AC上取一点P，使∠ABP=∠DCA，则∠CBP：∠ABP的值为 .

查看试题解析

三、解答题（本大题共9个小题，共72分）

17. 解方程组

(1)、 ${\begin{matrix} x + 3 y ＝ 8 \\ 5 x - 4 y ＝ 2 \end{matrix}$

(2)、 ${\begin{matrix} 3 (x - 1) ＝ y + 5 \\ 5 (y - 1) ＝ 3 (x + 5) \end{matrix}$

查看试题解析
18. 求满足不等式组 ${\begin{matrix} 3 x - 5 > 1 ① \\ 5 x - 18 \leq 12 ② \end{matrix}$ 的整数解.

查看试题解析
19. 如图，在 $△ A B C$ 中， $B D ⊥ A C$ 于点D，E为BC上一点，过E点作 $E F ⊥ A C$ ，垂足为F，过点D作 $D H / / B C$ 交AB于点H.

(1)、请你补全图形 $($ 不要求尺规作图 $)$ ；

(2)、求证： $∠ B D H = ∠ C E F$ .

查看试题解析
20. 2020年两会，总理点赞地摊经济，一夜之间，“摆摊”成了当下的潮流，即将大学毕业的小明也准备“摆摊”锻炼一下，经过他的调查，A、B两种小商品的批发价与市场零售价如下表所示：

A商品 B商品

批发价（元/件） 3 4

零售价（元/件） 5 7

小明从中豪小商品批发市场批发A、B两种商品共用了320元，两天他卖完这些A、B两种小商品共赚了230元，他批发的A、B两种商品分别是多少件？

查看试题解析
21. 夏季少年儿童溺水事件时有发生，为提高学生防溺水的自觉性和识别险情、紧急避险、遇险逃生的能力，某校举行了“防溺水安全知识竞赛”，全校2000名学生都参与了竞赛，为了解学生答题情况，随机抽取了部分学生的成绩，并把成绩x（分）分成五组：A组：50≤x＜60；B组：60≤x＜70；C组：70≤x＜80；D组：80≤x＜90；E组：90≤x＜100．
统计后绘制成如下两个统计图（不完整）．

(1)、直接填空：
①校本容量是， m的值为；

②在图2中，C组的扇形圆心角的度数为．

(2)、在图1中，补全直方图；

(3)、若学生成绩不低于80分确定为优秀，则全校估计有多少名学生的成绩为优秀？

查看试题解析
22. 某校为表彰在新冠病毒肺炎疫情期间在线学习表现优秀的学生，计划购买一批奖品．已知购买3件A种奖品和2件B种奖品共需84元；购买5件A种奖品和4件B种奖品共需148元．

(1)、求A、B两种奖品的单价各是多少？

(2)、若该校准备购买A、B两种奖品共50件，总费用不超过760元，则A种奖品最多购买多少件？

查看试题解析
23. 如图，CD∥EF，AC⊥AE，且∠α和∠β的度数满足方程组 ${\begin{matrix} 2 ∠ α + ∠ β ＝ 235 ° \\ ∠ β - ∠ α ＝ 70 ° \end{matrix}$

(1)、求∠α和∠β的度数．

(2)、求证：AB∥CD．

(3)、求∠C的度数．

查看试题解析
24. 新冠肺炎疫情期间，我市对学生进行了“停课不停学”的线上教学活动．某中学为了解这期间九年级学生数学学习的情况，开学后进行了两次诊断性练习．综合成绩由两次练习成绩组成，其中第一次练习成绩占40%，第二次练习成绩占60%．当综合成绩不低于96分时，该生数学学科综合评价为优秀．

(1)、小明同学的两次练习成绩之和为225分，综合成绩为113分，则他这两次练习成绩各得多少分？

(2)、如果小张同学第一次练习成绩为90分，综合成绩要达到优秀，他的第二次练习成绩至少要得多少分？

查看试题解析
25. 如图①，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）²+ $\sqrt{b - 2}$ =0，过C作CB⊥x轴于B．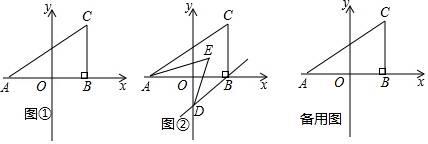

(1)、求三角形ABC的面积；

(2)、如图②，若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数；

(3)、在y轴上是否存在点P，使得三角形ACP和三角形ABC的面积相等？若存在，求出P点的坐标；若不存在，请说明理由．

查看试题解析

	A商品	B商品
批发价（元/件）	3	4
零售价（元/件）	5	7