湖北省宜城市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-03 类型：期末考试

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{2}$ 的绝对值是（）

A、﹣ $\sqrt{2}$ B、± $\sqrt{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
2. 方程组 ${\begin{matrix} x + y = 10 \\ 2 x + y = 16 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 6 \\ y = 4 \end{matrix}$ B、 ${\begin{matrix} x = 5 \\ y = 6 \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 6 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 8 \end{matrix}$

查看试题解析
3. 若 $m > n$ ，则下列不等式正确的是（）

A、 $m - 2 < n - 2$ B、 $- 8 m > - 8 n$ C、 $6 m < 6 n$ D、 $\frac{m}{4} > \frac{n}{4}$

查看试题解析
4. 下列哪个不等式与不等式 $5 x > 8 + 2 x$ 组成的不等式组的解集为 $\frac{8}{3} < x < 5$ （）

A、 $x + 5 < 0$ B、 $2 x > 10$ C、 $- x - 5 > 0$ D、 $3 x - 15 < 0$

查看试题解析
5. 下列无理数中，与3最接近的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{11}$ D、 $\sqrt{13}$

查看试题解析
6. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等.交易其一，金轻十三两.问金、银一枚各重几何？”.意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等.两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）

A、 ${\begin{array}{l} 11 x = 9 y \\ （ 10 y + x ） - （ 8 x + y ） = 13 \end{array}$ B、 ${\begin{array}{l} 10 y + x = 8 x + y \\ 9 x + 13 = 11 y \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y \\ （ 8 x + y ） - （ 10 y + x ） = 13 \end{array}$ D、 ${\begin{array}{l} 9 x = 11 y \\ （ 10 y + x ） - （ 8 x + y ） = 13 \end{array}$

查看试题解析
7. 下列调查中，最适合采用全面调查（普查）方式的是（）

A、对乘坐飞机的旅客是否携带违禁物品的调查 B、对七里花园社区每天丢弃塑料袋数量的调查 C、对宜城市辖区内汉江流域水质情况的调查 D、对宜城电视台“宜城记忆”栏目收视率的调查

查看试题解析
8. 在平面直角坐标系中，点P(－2，x²＋1)所在的象限是( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 如图，有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上。如果∠2=44°，那么∠1的度数是（）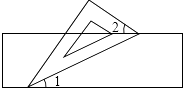

A、14° B、15° C、16° D、17°

查看试题解析
10. 如图，将长方形 $A B C D$ 沿对角线 $B D$ 折叠，点C落在点E处， $B E$ 交 $A D$ 于点F，已知 $∠ B D C = 65 °$ ，则 $∠ D F E$ 的度数为（）

A、32.5° B、25° C、50° D、65°

查看试题解析

二、填空题

11. 25的算术平方根是．

查看试题解析
12. 若a﹣3b=2，3a﹣b=6，则b﹣a的值为．

查看试题解析
13. 不等式 $3 x + 2 \geq - 5$ 的负整数解是.

查看试题解析
14. 在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为4，到y轴的距离为3，则点M的坐标是.

查看试题解析
15. 若关于x，y的方程组 ${\begin{array}{l} 3 x + 4 y = 8 \\ m x + (2 m - 1) y = 7 \end{array}$ 的解也是二元一次方程 $2 x - 3 y = 11$ 的解，则m的值为.

查看试题解析
16. 在同一平面内，设a、b、c是三条互相平行的直线，已知a与b的距离为4cm，b与c的距离为1cm，则a与c的距离为.

查看试题解析

三、解答题

17. 用消元法解方程组 ${\begin{array}{l} x - 3 y = 5 ① \\ 4 x - 3 y = 2 ② \end{array}$ 时,两位同学的解法如下:
解法一: 解法二:由②，得 $3 x + (x - 3 y) = 2$ , ③

由①-②,得 $3 x = 3$ . 把①代入③，得 $3 x + 5 = 2$ .

(1)、反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“ $\times$ ”.

(2)、请选择一种你喜欢的方法,完成解答.

查看试题解析
18. 在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三
角形叫做“格点三角形”，根据图形，回答下列问题.

(1)、图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的？

(2)、如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为(－3，4)，请写出格点三角形DEF各顶点的坐标，并求出三角形DEF的面积.

查看试题解析
19. 求不等式组的 ${\begin{array}{l} 4 x - 7 < 5 (x - 1) \\ \frac{x}{3} \leq 3 - \frac{x - 2}{2} \end{array}$ 整数解.

查看试题解析
20. 为增强学生体质，各学校普遍开展了阳光体育活动，某校为了解全校1000名学生每周课外体育活动时间的情况，随机调查了其中的50名学生，对这50名学生每周课外体育活动时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤x＜8小时的学生人数占24%．根据以上信息及统计图解答下列问题：

(1)、本次调查属于调查，样本容量是；

(2)、请补全频数分布直方图中空缺的部分；

(3)、求这50名学生每周课外体育活动时间的平均数；

(4)、估计全校学生每周课外体育活动时间不少于6小时的人数．

查看试题解析
21. 如图，AB∥CD，点E是CD上一点，∠AEC＝42°，EF平分∠AED交AB于点F，求∠AFE的度数.

查看试题解析
22. 如图，在 $△ A B C$ 中， $B D ⊥ A C$ 于点D，E为BC上一点，过E点作 $E F ⊥ A C$ ，垂足为F，过点D作 $D H / / B C$ 交AB于点H.

(1)、请你补全图形 $($ 不要求尺规作图 $)$ ；

(2)、求证： $∠ B D H = ∠ C E F$ .

查看试题解析
23. 为提高市民的环保意识，倡导“节能减排，绿色出行”，某市计划在城区投放一批“共享单车”这批单车分为A，B两种不同款型，其中A型车单价400元，B型车单价320元．

(1)、今年年初，“共享单车”试点投放在某市中心城区正式启动．投放A，B两种款型的单车共100辆，总价值36800元．试问本次试点投放的A型车与B型车各多少辆？

(2)、试点投放活动得到了广大市民的认可，该市决定将此项公益活动在整个城区全面铺开．按照试点投放中A，B两车型的数量比进行投放，且投资总价值不低于184万元．请问城区10万人口平均每100人至少享有A型车与B型车各多少辆？

查看试题解析
24. 如图1，在平面直角坐标系中，点O为坐标原点，点A(3a，2a)在第一象限，过点A向x轴作垂线，垂足为点B，连接OA，S△AOB=12，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN.

(1)、求a的值；

(2)、当0<t<2时，
①请探究∠ANM，∠OMN，∠BAN之间的数量关系，并说明理由；

②试判断四边形AMON的面积是否变化?若不变化，请求出其值；若变化，请说明理由。

(3)、当OM=ON时，请求出t的值。

查看试题解析
25. 为拓宽学生视野，引导学生主动适应社会，促进书本知识和生活经验的深度融合，我市某中学决定组织部分班级去赤壁开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．现有甲、乙两种大客车，它们的载客量和租金如表所示．

甲种客车
乙种客车
载客量/（人/辆）
30
42
租金/（元/辆）
300
400
学校计划此次研学旅行活动的租车总费用不超过3100元，为了安全，每辆客车上至少要有2名老师．

(1)、参加此次研学旅行活动的老师和学生各有多少人？

(2)、既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师，可知租用客车总数为辆；

(3)、你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．

查看试题解析

	甲种客车	乙种客车
载客量/（人/辆）	30	42
租金/（元/辆）	300	400