湖北省武汉市武昌区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2020-07-03 类型：期末考试
一、选择题
-
1. 在平面直角坐标系中，点（－1，2）在（ ）.A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 9的平方根是（ ）A、 -3 B、3 C、±3 D、813. 不等式组解集为 -1 ≤x < 1 ，下列在数轴上表示正确的是（ ）A、
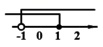B、
C、
D、
4. 在下列实数中，最小的是（ ）A、- B、- C、0 D、5. 如图，点 E 在 AD 的延长线上，下列条件中能判断 AB∥CD 的是（ ）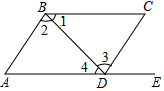
A、∠1=∠4 B、∠2=∠3 C、∠C=∠CDE D、∠C+∠CDA=180°6. 是二元一次方程 2x + ay = 4 的一组解，则 a 的值是（ ）A、1 B、0 C、2 D、－17. 下列调查中，适宜采用抽样调查方式的是 （ ）A、了解某校七年级（1）班同学的身高情况 B、企业招聘，对应聘人员进行面试 C、检测武汉市的空气质量 D、选出某校七年级（1）班短跑最快的学生参加校运动会8. 下列实数中，在 3 与 4 之间的数是（ ）A、 B、 C、 D、 -19. 如图，图①是一个四边形纸条 ABCD，其中 AB∥CD，E，F 分别为边 AB，CD 上的两个点，将纸条 ABCD 沿 EF 折叠得到图②，再将图②沿 DF 折叠得到图③，若在图③中，∠FEM=26°，则∠EFC 的度数为（ ）
A、52° B、64° C、102° D、128°10. 在平面直角坐标系中，A（m，4），B（2，n），C（2，4－m），其中 m+n=2，并且2 ≤ 2m+n ≤ 5， 则△ABC 面积的最大值为（ ）A、1 B、2 C、3 D、6二、填空题
-
11. 计算： ．12. 已知10个数据：0，1，2，6，2，1，2，3，0，3，其中 2 出现的频数为.13. 如图，直线 AB ，CD 相交于点O ，若∠EOC ：∠EOD=4 ：5 ，OA平分∠EOC ，则∠BOE=.
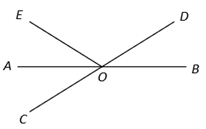14. 如图，点 B 在点 C 北偏东 39°方向，点 B 在点 A 北偏西 23°方向，则∠ABC 的度数为 .
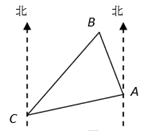15. 若一个长方形的长减少 7cm，宽增加 4cm 成为一个正方形，并且得到的正方形与原长 方形面积相等，则原长方形的长为-cm.16. 已知关于 x 的不等式 x－a<0 的最大整数解为 3a+5，则 a=.三、解答题
-
17. 解方程组18. 解不等式组19. 填空完成推理过程：
如图，∠1=∠2，∠A=∠D， 求证：∠B=∠C.
证明：∵∠1=∠2（已知），
∠1=∠3（ ），
∴∠2=∠3（等量代换）.
∴AF∥_▲_（ ）.
∴∠D=∠4（两直线平行，同位角相等 ）.
∵∠A=∠D（已知），
∴∠A=∠4（等量代换）.
∴AB∥CD（内错角相等，两直线平行）.
∴∠B=∠C（ ）.
20. 有 40 支队 520 名运动员参加篮球、足球比赛，其中每支篮球队 10 人，每支足球队 18人，每名运动员只能参加一项比赛.篮球队、足球队各有多少支参赛？21. 为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校100名学生进行调查，要求每名学生只选出一类自己最喜爱的节目，根据调查结果 绘制了不完整的条形图和扇形统计图（如图），
根据图中提供的信息，解答下列问题：
(1)、这次抽样调查的女生人数是人；(2)、扇形统计图中， “A”组对应的圆心角度数为 ， 并将条形图中补充完整；(3)、若该校有 1800 名学生，试估计全校最喜欢新闻和戏曲的学生一共有多少人？22. 如图，长青农产品加工厂与 A，B 两地有公路、铁路相连.这家工厂从 A 地购买一批原料甲运回工厂，经过加工后制成产品乙运到 B 地，其中原料甲和产品乙的重量都是正整数.已知铁路运价为 2 元/（吨·千米），公路运价为 8 元/（吨·千米）.
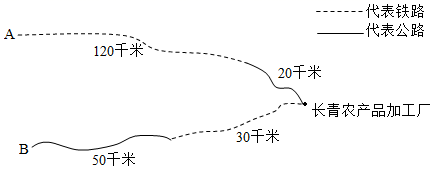(1)、若由 A 到 B 的两次运输中，原料甲比产品乙多 9 吨，工厂计划支出铁路运费超 过 5700 元，公路运费不超过 9680 元.问购买原料甲有哪几种方案，分别是多少吨？(2)、由于国家出台惠农政策，对运输农产品的车辆免收高速通行费，并给予一定的 财政补贴，综合惠农政策后公路运输价格下降 m（ 0 < m < 4 且 m 为整数）元， 若由 A 到 B 的两次运输中，铁路运费为 5760 元，公路运费为 5100 元，求 m 的 值.23. 如图 1，AB∥CD，点 E 在 AB 上，点 M 在 CD 上，点 F 在直线 AB，CD 之间，连接 EF、FM， EF⊥FM，∠CMF=140°.
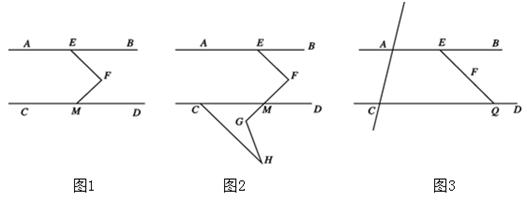(1)、直接写出∠AEF 的度数为 ；(2)、如图 2，延长 FM 到 G，点 H 在 FG 的下方，连接 GH，CH，若∠FGH=∠H+90°， 求∠MCH 的度数；(3)、如图 3，作直线 AC，延长 EF 交 CD 于点 Q，P 为直线 AC 上一动点，探究∠PEQ，∠PQC 和∠EPQ 的数量关系，请直接给出结论.（题中所有角都是大于 0°小于 180°的角）24. 在平面直角坐标系中，点 A（a，6），B（4，b），
(1)、若 a，b 满足 (a + b - 5)2 + = 0 ，①求点 A，B 的坐标；
②点 D 在第一象限，且点 D 在直线 AB 上，作 DC⊥x 轴于点 C，延长 DC 到 P 使 得 PC=DC，若△PAB 的面积为 10，求 P 点的坐标；
(2)、如图，将线段 AB 平移到 CD，且点 C 在 x 轴负半轴上，点 D 在 y 轴负半轴上， 连接 AC 交 y 轴于点 E，连接 BD 交 x 轴于点 F，点 M 在 DC 延长线上，连 EM，3∠MEC+∠CEO=180°，点 N 在 AB 延长线上，点 G 在 OF 延长线上，∠NFG= 2∠NFB，请探究∠EMC 和∠BNF 的数量关系，给出结论并说明理由.