湖北省武汉市江夏区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-03 类型：期末考试

进入出卷网下载

一、选择题

1. 在下列所给出坐标的点中，在第二象限的是（）

A、（2，3） B、（﹣2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
2. 下图所表示的不等式组的解集为（）

A、x＞3 B、-2＜x＜3 C、x＞-2 D、-2＞x＞3

查看试题解析
3. 下列选项中的整数，与 $\sqrt{17}$ 最接近的是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 下列问题不适合用全面调查的是（）

A、旅客上飞机前的安检： B、调查春节联欢晚会的收视率： C、了解某班学生的身高情况： D、企业招聘，对应试人员进行面试.

查看试题解析
5. 如图，点E在CD的延长线上，下列条件中不能判定AB∥CD的是（）

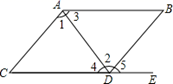A、∠1=∠2 B、∠3=∠4 C、∠5=∠B D、∠B +∠BDC=180°

查看试题解析
6. 谢老师对班上某次数学模拟考试成绩进行统计，绘制了如图所示的统计图，根据图中给出的信息，这次考试成绩达到A等级的人数占总人数的（）

A、6% B、10% C、20% D、25%

查看试题解析
7. 如图， $A ， B$ 的坐标为 $(2 ， 0)$ ， $(0 ， 1)$ ，若将线段 $A B$ 平移至 $A_{1} B_{1}$ ，则 $a + b$ 的值为（）

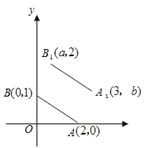A、5 B、4 C、3 D、2

查看试题解析
8. 由美国单方面挑起的贸易战严重影响了市场经济，某种国外品牌洗农机按原价降价 $a$ 元后，再次降价20%现售价为b元，则原售价为（）

A、 $(a + \frac{5}{4} b)$ 元 B、 $(a + \frac{4}{5} b)$ 元 C、 $(b + \frac{5}{4} a)$ 元 D、 $(b + \frac{4}{5} a)$ 元

查看试题解析
9. 若实数3是不等式2x–a–2<0的一个解，则a可取的最小正整数为（）

A、2 B、3 C、4 D、5

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ B = ∠ D$ ，延长 $B A$ 至E，连接 $C E$ 交 $A D$ 于F， $∠ E A D$ 和 $∠ E C D$ 的角平分线相交于点P.若 $∠ E = 60 °$ ， $∠ A P C = 70 °$ ，则 $∠ D$ 的度数是（）

A、80° B、75° C、70° D、60°

查看试题解析

二、填空题

11. ①9平方根是；② $\sqrt{\frac{1}{4}} =$ ；③若 $| a - 1 | = a - 1$ ，则a的取值范围是.

查看试题解析
12. 如图是一个会场的台阶的截面图，要在上面铺上地毯，则所需地毯的长度是.

查看试题解析
13. 某校开展“未成年人普法”知识竞赛，共有20道题，答对一题记10分，答错（或不答）一题记 $- 5$ 分.小明参加本次竞赛的得分超过100分，他至少答对了题；

查看试题解析
14. 如图，直线 $A B ∥ C D ∥ E F$ ， $∠ B = 30 °$ ， $∠ C = 135 °$ ，则 $∠ C G B =$ ；

查看试题解析
15. 如图，平面直角坐标系中的图案是由五个边长为1的正方形组成的.A（a，0），B（3，3），连接AB的线段将图案的面积分成相等的两部分，则a的值是：；

查看试题解析
16. 若关于x、y的二元一次方程组 ${\begin{matrix} 2 x + y = 3 k - 1 \\ x + 2 y = - 2 \end{matrix}$ 的解满足x+y＞1，则k的取值范围是．

查看试题解析

三、解答题

17.

(1)、解方程组： ${\begin{array}{l} 2 x + y = 11 \\ x - y = - 2 \end{array}$ ；

(2)、解下列不等式 $\frac{2 x - 1}{3} - 1 \leq \frac{3 x - 4}{6}$ .

查看试题解析
18. 如图，已知 $A B ∥ C D$ ， $∠ B + ∠ D = 180 °$ ，求证： $B C ∥ D E$ .

查看试题解析
19. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：今有鸡兔同笼，上有三十五头，下有九四十足，问鸡兔各几何？你能用二元一次方程组表示题中的数量关系并解决问题吗？

查看试题解析
20. 学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况，采用抽样的方法在七年级选取了一个班的同学，通过问卷调查，收集数据、整理数据，制作了如下两个整统计图，请根据下面两个不完整的统计图分析数据，回答以下问题：

(1)、七年级的这个班共有学生人，图中 $a =$ ， $b =$ ，在扇形统计图中，“体育”类电视节目对应的圆心角为：.

(2)、补全条形统计图；

(3)、根据抽样调查的结果，估算该校1750名学生中大约有多少人喜欢“娱乐”类电视节目？

查看试题解析
21. 如图，已知直线 $a ∥ b$ ，点 $A$ 在直线 $a$ 上，点 $B$ 、 $C$ 在直线 $b$ 上，点 $D$ 在线段 $B C$ 上. $A B$ 平分 $∠ M A D$ ， $A C$ 平分 $∠ N A D$ ， $∠ 1 = ∠ 2$ ，求证： $D E ⊥ A C$ .

查看试题解析
22. 2019年“519（我要走）全国徒步日（江夏站）”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会（活动主办方）为了奖励活动中取得了好成绩的参赛选手，计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元，乙种纪念品每件售价80元.

(1)、如果购买甲、乙两种纪念品一共花费了9600元，求购买甲、乙两种纪念品各是多少件？

(2)、设购买甲种纪念品 $m$ 件，如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍，并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案？哪一种方案所需总费用最少？最少总费用是多少元？

查看试题解析
23. 已知 $Δ A B C$ 中，点 $D$ 是 $A C$ 延长线上的一点，过点 $D$ 作 $D E ∥ B C$ ， $D G$ 平分 $∠ A D E$ ， $B G$ 平分 $∠ A B C$ ， $D G$ 与 $B G$ 交于点 $G$ .

(1)、如图1，若 $∠ A C B = 90 °$ ， $∠ A = 50 °$ ，直接求出 $∠ G$ 的度数：；

(2)、如图2，若 $∠ A C B \neq 90 °$ ，试判断 $∠ G$ 与 $∠ A$ 的数量关系，并证明你的结论；

(3)、如图3，若 $F E ∥ A D$ ，求证： $∠ D F E = \frac{1}{2} ∠ A B C + ∠ G$ .

查看试题解析
24. 如图1，点 $A (a ， 0)$ 、 $B (b ， 0)$ ，其中 $a$ 、 $b$ 满足 ${(3 a + b)}^{2} + \sqrt{b - a - 4} = 0$ ，将点A、B分别向上平移2个单位，再向右平移1个单位至C、D，连接 $A C$ 、 $B D$ .

(1)、直接写出点D的坐标：；

(2)、连接 $A D$ 交 $O C$ 于一点 $F$ ，求 $\frac{C F}{O F}$ 的值：

(3)、如图2，点 $M$ 从 $O$ 点出发，以每秒1个单位的速度向上平移运动，同时点 $N$ 从 $B$ 点出发，以每秒2个单位的速度向左平移运动，设射线 $D N$ 交 $y$ 轴于 $F$ .问 $S_{Δ F M D} - S_{Δ O F N}$ 的值是否为定值？如果是定值，请求出它的值；如果不是定值，请说明理由.

查看试题解析