湖北省恩施市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-03 类型:期末考试
一、选择题
-
1. 的算术平方根为( )A、 B、 C、 D、2. 已知m,n满足方程组 ,则m+n的值为( )A、3 B、﹣3 C、﹣2 D、23. 已知a>2a,那么对于a的判断正确的是( )A、是正数 B、是负数 C、是非正数 D、是非负数4. 已知不等式组 ,其解集正确的是( )A、﹣1≤x<3 B、﹣1<x≤3 C、x>3 D、x≤﹣15. 实数a,b在数轴上的位置如图所示,则化简 - +b的结果是( )
 A、1 B、b+1 C、2a D、1-2a6. 某学生某月有零花钱a元,其支出情况如图所示,那么下列说法不正确的是( )
A、1 B、b+1 C、2a D、1-2a6. 某学生某月有零花钱a元,其支出情况如图所示,那么下列说法不正确的是( ) A、该学生捐赠款为0.6a元 B、捐赠款所对应的圆心角为240° C、捐赠款是购书款的2倍 D、其他消费占10%7. 在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
A、该学生捐赠款为0.6a元 B、捐赠款所对应的圆心角为240° C、捐赠款是购书款的2倍 D、其他消费占10%7. 在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )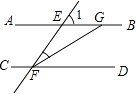 A、122° B、151° C、116° D、97°9. 如图, 的坐标为 , ,若将线段 平移至 ,则 的值为( )
A、122° B、151° C、116° D、97°9. 如图, 的坐标为 , ,若将线段 平移至 ,则 的值为( )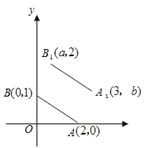 A、5 B、4 C、3 D、210. 将某图形的各顶点的横坐标减去3,纵坐标保持不变,可将该图形( )A、横向向右平移3个单位 B、横向向左平移3个单位 C、纵向向上平移3个单位 D、纵向向下平移3个单位11. 如果关于 的方程组 的解是正数,那a的取值范围是( )A、 B、 C、 D、无解12. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )
A、5 B、4 C、3 D、210. 将某图形的各顶点的横坐标减去3,纵坐标保持不变,可将该图形( )A、横向向右平移3个单位 B、横向向左平移3个单位 C、纵向向上平移3个单位 D、纵向向下平移3个单位11. 如果关于 的方程组 的解是正数,那a的取值范围是( )A、 B、 C、 D、无解12. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )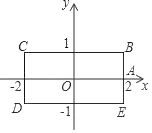 A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)
A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)二、填空题
-
13. 计算: ﹣|﹣2|=.14. x的 与12的差不小于6,用不等式表示为 .15.
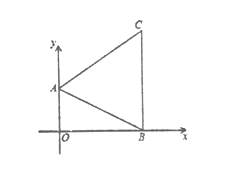
如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
 16. 如图,小章利用一张左、右两边已经破损的长方形纸片 做折纸游戏,他将纸片沿 折叠后,D、C两点分别落在 、 的位置,并利用量角器量得 ,则 等于度.
16. 如图,小章利用一张左、右两边已经破损的长方形纸片 做折纸游戏,他将纸片沿 折叠后,D、C两点分别落在 、 的位置,并利用量角器量得 ,则 等于度.
三、解答题
-
17.(1)、解方程组:(2)、解不等式组 ,并将解集在数轴上表示出来.18. 已知3既是x-1的平方根,又是x-2y+1的立方根,求x2-y2的平方根.19. 如图,直线 ,射线 与直线a相交于点C,过点D作 于点E,已知 ,求 的度数.
 20. “中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
20. “中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题: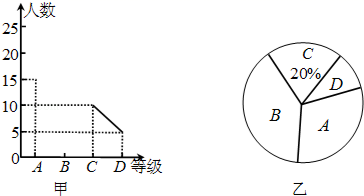 (1)、共抽取了多少个学生进行调查?(2)、将图甲中的折线统计图补充完整.(3)、求出图乙中B等级所占圆心角的度数.21. 如图所示,三角形 (记作 )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , ,先将 向上平移3个单位长度,再向右平移2个单位长度,得到 .
(1)、共抽取了多少个学生进行调查?(2)、将图甲中的折线统计图补充完整.(3)、求出图乙中B等级所占圆心角的度数.21. 如图所示,三角形 (记作 )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , ,先将 向上平移3个单位长度,再向右平移2个单位长度,得到 . (1)、在图中画出 ;(2)、点 , , 的坐标分别为、、;(3)、若y轴上有一点P,使 与 面积相等,求出P点的坐标.22. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.(1)、求A、B两种型号家用净水器各购进了多少台(2)、为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)
(1)、在图中画出 ;(2)、点 , , 的坐标分别为、、;(3)、若y轴上有一点P,使 与 面积相等,求出P点的坐标.22. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.(1)、求A、B两种型号家用净水器各购进了多少台(2)、为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)