湖北省鄂州市梁子湖区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-03 类型:期末考试
一、选择题
-
1. 下列实数中,是无理数的为( )A、 B、 C、π D、2. 若a>b,则下列不等式变形正确的是( )A、a+5<b+5 B、 C、3a>3b D、-4a > -4b3. 如图是运动员冰面上表演的图案,下列四个选项中,能由原图通过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列调查中,适合用普查方式的是( )A、了解某班学生“50米跑”的成绩 B、了解一批灯泡的使用寿命 C、了解一批炮弹的杀伤半径 D、调查长江流域的水污染情况5. 若 是下列某二元一次方程组的解,则这个方程组为( )A、 B、 C、 D、6. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、
4. 下列调查中,适合用普查方式的是( )A、了解某班学生“50米跑”的成绩 B、了解一批灯泡的使用寿命 C、了解一批炮弹的杀伤半径 D、调查长江流域的水污染情况5. 若 是下列某二元一次方程组的解,则这个方程组为( )A、 B、 C、 D、6. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、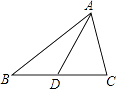 B、
B、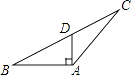 C、
C、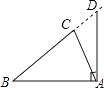 D、
D、 7. 点 的坐标为 ,且到两坐标轴的距离相等,则点 的坐标为( )A、 B、 C、 D、 或8. 如图,在矩形ABCD中放入6个全等的小矩形,所标尺寸如图所示,设小矩形的长为a,宽为b,则可得方程组( )
7. 点 的坐标为 ,且到两坐标轴的距离相等,则点 的坐标为( )A、 B、 C、 D、 或8. 如图,在矩形ABCD中放入6个全等的小矩形,所标尺寸如图所示,设小矩形的长为a,宽为b,则可得方程组( )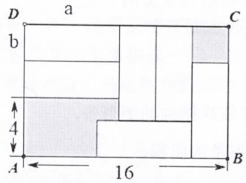 A、 B、 C、 D、9. 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )
A、 B、 C、 D、9. 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个10. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )
A、1个 B、2个 C、3个 D、4个10. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )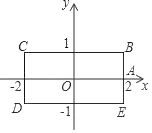 A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)
A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)二、填空题
-
11. 的算术平方根是 ,﹣2的相反数是 ,的绝对值是 .12. 如图,把一张宽度相等的纸条按图上所示的方式折叠,则∠1的度数等于°.
 13. 从鱼池的不同地方捞出100条鱼,在鱼的身上做上记号,然后把鱼放回鱼池.过一段时间后,在同样的地方再捞出50条鱼,其中带有记号的鱼有2条,则可以估计整个鱼池约有鱼条.14. 如图,在宽为21m,长为31m的矩形地面上修建两条同样宽为1m的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为m2.
13. 从鱼池的不同地方捞出100条鱼,在鱼的身上做上记号,然后把鱼放回鱼池.过一段时间后,在同样的地方再捞出50条鱼,其中带有记号的鱼有2条,则可以估计整个鱼池约有鱼条.14. 如图,在宽为21m,长为31m的矩形地面上修建两条同样宽为1m的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为m2. 15. 如图,三角形ABC中,∠BAC=70°, D是射线BC上一点(不与点B,C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为.
15. 如图,三角形ABC中,∠BAC=70°, D是射线BC上一点(不与点B,C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为. 16. 若关于x的不等式组 的整数解共有4个,则a的取值范围是 .
16. 若关于x的不等式组 的整数解共有4个,则a的取值范围是 .三、解答题
-
17. 解下列方程组与不等式组.(1)、(2)、18. 如图,数轴的正半轴上有A,B,C三点,表示1和 的对应点分别为A,B,点B到点A的距离与点C到原点的距离相等,设点C所表示的数为x.
 (1)、请你直接写出 的值;(2)、求 的平方根.19. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)、请你直接写出 的值;(2)、求 的平方根.19. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点. (1)、请画出平移后的△A′B′C′(不写画法),并直接写出点B′的坐标:B′();(2)、若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是();(3)、求出△ABC的面积.20. 某区教育部门准备在七年级开设兴趣课堂,以丰富学生课余生活.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
(1)、请画出平移后的△A′B′C′(不写画法),并直接写出点B′的坐标:B′();(2)、若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是();(3)、求出△ABC的面积.20. 某区教育部门准备在七年级开设兴趣课堂,以丰富学生课余生活.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题: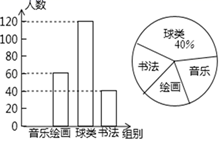 (1)、此次共调查了名同学;(2)、将条形图补充完整 , 计算扇形统计图中音乐部分的圆心角的度数是;(3)、如果该区七年级共有2 000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?21. 直线 ∥ ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接
(1)、此次共调查了名同学;(2)、将条形图补充完整 , 计算扇形统计图中音乐部分的圆心角的度数是;(3)、如果该区七年级共有2 000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?21. 直线 ∥ ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接 PA、PC. (1)、如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为(2)、如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为(3)、如图3,求证:∠P=∠PAB+∠PCD;(4)、如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为22. 甲、乙二人解关于x,y的方程组 甲正确地解出 而乙因把c抄错了,结果解得 求出a,b,c的值,并求乙将c抄成了何值?23. 某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
PA、PC. (1)、如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为(2)、如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为(3)、如图3,求证:∠P=∠PAB+∠PCD;(4)、如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为22. 甲、乙二人解关于x,y的方程组 甲正确地解出 而乙因把c抄错了,结果解得 求出a,b,c的值,并求乙将c抄成了何值?23. 某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表: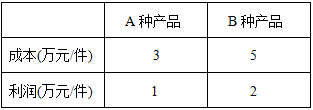 (1)、若工厂计划获利14万元,问A、B两种产品应分别生产多少件?(2)、若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?(3)、在(2)条件下,哪种方案获利最大?并求最大利润.24. 如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足 ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
(1)、若工厂计划获利14万元,问A、B两种产品应分别生产多少件?(2)、若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?(3)、在(2)条件下,哪种方案获利最大?并求最大利润.24. 如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足 ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点. (1)、求C点坐标;(2)、如图2,连接DE,若DE AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;(3)、如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中, 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
(1)、求C点坐标;(2)、如图2,连接DE,若DE AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;(3)、如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中, 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.