山东省临沂市2020届高三数学一模试卷
试卷更新日期:2020-07-03 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知复数 , 在复平面内对应的点分别为 , ,则 的共轭复数为( )A、 B、 C、 D、3. 若 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知向量 ,其中 与 是相反向量,且 , ,则 ( )A、 B、 C、2 D、5. 已知 , , ,则( )A、 B、 C、 D、6. 已知函数 , ,当 时, 取得最大值b,则函数 的大致图象为( )A、
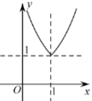 B、
B、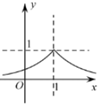 C、
C、 D、
D、 7. 《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积为粟几何?”,意思是“有粟若干,堆积在平地上,它底圆周长为12丈,高为1丈,问它的体积和粟各为多少?”如图,主人意欲卖掉该堆粟,已知园周率约为3,一斛粟的体积约为2700立方寸(单位换算:1立方丈 立方寸),一斛粟米卖270钱,一两银子1000钱,则主人卖后可得银子( )
7. 《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积为粟几何?”,意思是“有粟若干,堆积在平地上,它底圆周长为12丈,高为1丈,问它的体积和粟各为多少?”如图,主人意欲卖掉该堆粟,已知园周率约为3,一斛粟的体积约为2700立方寸(单位换算:1立方丈 立方寸),一斛粟米卖270钱,一两银子1000钱,则主人卖后可得银子( ) A、200两 B、240两 C、360两 D、400两8. 点 为抛物线 上任意一点,点 为圆 上任意一点,若函数 的图象恒过定点 ,则 的最小值为( )A、 B、 C、3 D、
A、200两 B、240两 C、360两 D、400两8. 点 为抛物线 上任意一点,点 为圆 上任意一点,若函数 的图象恒过定点 ,则 的最小值为( )A、 B、 C、3 D、二、多选题
-
9. 下列结论正确的是( )A、若 ,则 B、若 ,则 C、“ , ”的否定是“ , ” D、将函数 的图象向左平移 个单位长度,所得图象关于原点对称10. 某同学在微信上查询到近十年全国高考报名人数、录取人数和山东夏季高考报名人数的折线图,其中2019年的录取人数被遮挡了.他又查询到近十年全国高考录取率的散点图,结合图表中的信息判定下列说法正确的是( )

 A、全国高考报名人数逐年增加 B、2018年全国高考录取率最高 C、2019年高考录取人数约820万 D、2019年山东高考报名人数在全国的占比最小11. 在 中,角A,B,C的对边分别为a,b,c,若 , , ,则下列结论正确的是( )A、 B、 C、 D、12. 如图,点E为正方形 边 上异于点C,D的动点,将 沿 翻折成 ,在翻折过程中,下列说法正确的是( )
A、全国高考报名人数逐年增加 B、2018年全国高考录取率最高 C、2019年高考录取人数约820万 D、2019年山东高考报名人数在全国的占比最小11. 在 中,角A,B,C的对边分别为a,b,c,若 , , ,则下列结论正确的是( )A、 B、 C、 D、12. 如图,点E为正方形 边 上异于点C,D的动点,将 沿 翻折成 ,在翻折过程中,下列说法正确的是( )
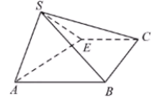 A、存在点E和某一翻折位置,使得 B、存在点E和某一翻折位置,使得 平面 C、存在点E和某一翻折位置,使得直线 与平面 所成的角为45° D、存在点E和某一翻折位置,使得二面角 的大小为60°
A、存在点E和某一翻折位置,使得 B、存在点E和某一翻折位置,使得 平面 C、存在点E和某一翻折位置,使得直线 与平面 所成的角为45° D、存在点E和某一翻折位置,使得二面角 的大小为60°三、填空题
-
13. 三名旅游爱好者商定,新冠肺炎疫情全面结束后,前往湖北省的武汉、宜昌、黄冈三个城市旅游.如果三人均等可能的前往上述三个城市之一,则他们选择同一个城市的概率是.14. 若 展开式中的各项系数的和为1024,则常数项为 .15. 已知函数 ,若方程 有两个不相等的实根,则实数a取值范围是 .
四、双空题
-
16. 已知双曲线 的一条渐近线方程为 ,左、右焦点分别为 , ,点 在双曲线上,且 ,则该双曲线的离心率为 , .
五、解答题
-
17. 记 为数列 的前 项和,已知 , .(1)、求数列 的通项公式;(2)、若 ,求满足 的正整数n的最大值.18. 已知函数 满足下列4个条件中的3个,4个条件依次是:① ,②周期 ,③过点 ,④ .(1)、写出所满足的3个条件的序号(不需要说明理由),并求 的解析式;(2)、求函数 的图象与直线 相邻两个交点间的最短距离.19. 如图,斜三棱柱 中, 是边长为2的正三角形, 为 的中点, 平面 ,点 在 上, , 为 与 的交点,且 与平面 所成的角为 .
 (1)、求证: 平面 ;(2)、求二面角 的正弦值.20. 动点P在椭圆 上,过点P作x轴的垂线,垂足为A,点 满足 ,已知点B的轨迹是过点 的圆.(1)、求椭圆C的方程;(2)、设直线l与椭圆C交于M,N两点(M,N在x轴的同侧), , 为椭圆的左、右焦点,若 ,求四边形 面积的最大值.21. 2020年新冠肺炎疫情暴发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做岀了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分(满分100分)数据统计结果如图:
(1)、求证: 平面 ;(2)、求二面角 的正弦值.20. 动点P在椭圆 上,过点P作x轴的垂线,垂足为A,点 满足 ,已知点B的轨迹是过点 的圆.(1)、求椭圆C的方程;(2)、设直线l与椭圆C交于M,N两点(M,N在x轴的同侧), , 为椭圆的左、右焦点,若 ,求四边形 面积的最大值.21. 2020年新冠肺炎疫情暴发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做岀了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分(满分100分)数据统计结果如图: (1)、若此次知识竞答得分 整体服从正态分布,用样本来估计总体,设 , 分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求 , 的值( , 的值四舍五入取整数),并计算 ;(2)、在(1)的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于 的获得1次抽奖机会,得分不低于 的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为 ,抽到36元红包的概率为 .已知高三某同学是这次活动中的幸运者,记 为该同学在抽奖中获得红包的总金额,求 的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
(1)、若此次知识竞答得分 整体服从正态分布,用样本来估计总体,设 , 分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求 , 的值( , 的值四舍五入取整数),并计算 ;(2)、在(1)的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于 的获得1次抽奖机会,得分不低于 的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为 ,抽到36元红包的概率为 .已知高三某同学是这次活动中的幸运者,记 为该同学在抽奖中获得红包的总金额,求 的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.参考数据: ; ; .
22. 已知函数 , , .(1)、设 ,求 在 上的最大值;(2)、设 ,若 的极大值恒小于0,求证: .
-