山东省聊城市2020届高三数学高考模拟(一)试卷
试卷更新日期:2020-07-03 类型:高考模拟
一、单选题
-
1. 已知集合 ,则集合 中元素的个数为( )A、1 B、2 C、3 D、42. 已知复数 满足 ,则复数z的共轭复数为( )A、 B、 C、 D、3. “ ”是“ 为真命题”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知 ,则 ( )A、 B、 C、 D、5. 将某校高一3班全体学生分成三个小组分别到三个不同的地方参加植树活动,若每个学生被分到三个小组的概率都相等,则这个班的甲,乙两同学分到同一个小组的概率为( )A、 B、 C、 D、6. 数列1,6,15,28,45,...中的每一项都可用如图所示的六边形表示出来,故称它们为六边形数,那么第10个六边形数为( )
 A、153 B、190 C、231 D、2767. 正方体 的棱长为1,点M是棱 的中点,点 都在球O的球面上,则球O的表面积为( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,为了纪念数学家高斯,人们把函数 称为高斯函数,其中 表示不超过x的最大整数.设 ,则函数 的所有零点之和为( )A、-1 B、0 C、1 D、2
A、153 B、190 C、231 D、2767. 正方体 的棱长为1,点M是棱 的中点,点 都在球O的球面上,则球O的表面积为( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,为了纪念数学家高斯,人们把函数 称为高斯函数,其中 表示不超过x的最大整数.设 ,则函数 的所有零点之和为( )A、-1 B、0 C、1 D、2二、多选题
-
9. 下列说法正确的是( )A、回归直线一定经过样本点的中心 B、若两个具有线性相关关系的变量的相关性越强,则线性相关系数 的值越接近于1 C、在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高 D、在线性回归模型中,相关指数 越接近于1,说明回归模型的拟合效果越好10. 若双曲线 的实轴长为6,焦距为10,右焦点为F,则下列结论正确的是( )A、C的渐近线上的点到 距离的最小值为4 B、C的离心率为 C、C上的点到 距离的最小值为2 D、过F的最短的弦长为11. 已知直线 与抛物线 相交于 两点,点 是抛物线C的准线与以 为直径的圆的公共点,则下列结论正确的是( )A、 B、 C、 D、 的面积为12. 若实数 ,则下列不等式中一定成立的是( )A、 B、 C、 D、
三、填空题
-
13. 已知 的展开式中 的系数为 ,则实数14. 若函数 在 上单调递增,则实数a的取值范围为15. 已知 ,且 ,则向量 与 的夹角
四、双空题
-
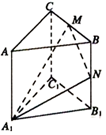
16. 点 分别为三棱柱 的棱 的中点,设 的面积为 ,平面 截三棱柱 所得截面面积为 ,五棱锥 的体积为 ,三棱柱 的体积为 ,则 , .
五、解答题
-
17. 这三个条件中任选一个,补充在下面问题中,并给出解答.
设等差数列 的前 项和为 ,数列 的前 项和为 ,_______, ,若对于任意 都有 ,且 ( 为常数),求正整数 的值.
18. 在平面四边形 中, .(1)、求 的面积;(2)、设M为 的中点,且 ,求四边形 周长的最大值.19. 如图,在四边形 中, ,以 为折痕把 折起,使点A到达点P的位置,且 . (1)、证明: 平面 ;(2)、若M为 的中点,二面角 等于60°,求直线 与平面 所成角的正弦值.20. 已知椭圆 的长轴长为4,右焦点为F,且椭圆C上的点到点F的距离的最小值与最大值的积为1,圆 与 轴交于 两点.(1)、求椭圆C的方程;(2)、动直线 与椭圆C交于 两点,且直线l与圆O相切,求 的面积与 的面积乘积的取值范围.21. 2020年春节期间,武汉市爆发了新型冠状病毒肺炎疫情,在党中央的坚强领导下,全国人民团结一心,众志成城,共同抗击疫情.某中学寒假开学后,为了普及传染病知识,增强学生的防范意识,提高自身保护能力,校委会在全校学生范围内,组织了一次传染病及个人卫生相关知识有奖竞赛(满分100分),竞赛奖励规则如下,得分在 内的学生获三等奖,得分在 内的学生获二等奖,得分在 内的学生获一等奖,其他学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
(1)、证明: 平面 ;(2)、若M为 的中点,二面角 等于60°,求直线 与平面 所成角的正弦值.20. 已知椭圆 的长轴长为4,右焦点为F,且椭圆C上的点到点F的距离的最小值与最大值的积为1,圆 与 轴交于 两点.(1)、求椭圆C的方程;(2)、动直线 与椭圆C交于 两点,且直线l与圆O相切,求 的面积与 的面积乘积的取值范围.21. 2020年春节期间,武汉市爆发了新型冠状病毒肺炎疫情,在党中央的坚强领导下,全国人民团结一心,众志成城,共同抗击疫情.某中学寒假开学后,为了普及传染病知识,增强学生的防范意识,提高自身保护能力,校委会在全校学生范围内,组织了一次传染病及个人卫生相关知识有奖竞赛(满分100分),竞赛奖励规则如下,得分在 内的学生获三等奖,得分在 内的学生获二等奖,得分在 内的学生获一等奖,其他学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图. (1)、现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;(2)、若该校所有参赛学生的成绩X近似服从正态分布 ,其中 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
(1)、现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;(2)、若该校所有参赛学生的成绩X近似服从正态分布 ,其中 为样本平均数的估计值,利用所得正态分布模型解决以下问题:(i)若该校共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机抽取3名学生进行座谈,设其中竞赛成绩在64分以上的学生数为 ,求随机变量 的分布列和均值.
附:若随机变量 服从正态分布 ,则 , , .
22. 已知函数 .(1)、证明:当 时,函数 有唯一的极值点;(2)、设 为正整数,若不等式 在 内恒成立,求 的最大值.
-