山东省济南市2020届高三数学二模试卷

试卷更新日期：2020-07-03 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $α$ 为第四象限角，则 $\cos α = \frac{5}{13}$ ，则 $s i n α =$ （）

A、 $- \frac{12}{13}$ B、 $\frac{12}{13}$ C、 $- \frac{5}{12}$ D、 $\frac{5}{12}$

查看试题解析
2. 已知 $x, y \in R$ ，集合 $A = {1, 2^{x}}$ ， $B = {x, y}$ ， $A \cap B = {\frac{1}{2}}$ ，则 $x y =$ （）

A、-1 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
3. 已知抛物线 $x^{2} = 4 y$ 的焦点为F，点P在抛物线上且横坐标为4，则 $| P F | =$ （）

A、2 B、3 C、5 D、6

查看试题解析
4. 十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目，按照国际田径联合会制定的田径运动全能评分表计分，然后将各个单项的得分相加，总分多者为优胜．下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图．

下列说法错误的是（）

A、在100米项目中，甲的得分比乙高 B、在跳高和标枪项目中，甲、乙的得分基本相同 C、甲的各项得分比乙更均衡 D、甲的总分高于乙的总分

查看试题解析
5. 已知函数 $f (x) = {\begin{array}{l} - x^{2} + 2 x - 1 ， x \leq 1 \\ | x - 1 | ， x > 1 \end{array}$ ，若 $f (a^{2} - 4) > f (3 a) ，$ ，则实数a的取值范围是（）

A、 $(- 4 ， 1)$ B、 $(- \infty ， - 4) \cup (1 ， + \infty)$ C、 $(- 1 ， 4)$ D、 $(- \infty ， - 1) \cup (4 ， + \infty)$

查看试题解析
6. 任何一个复数 $z = a + b i$ （其中 $a, b \in R$ ，i为虚数单位）都可以表示成 $z = r (\cos θ + i \sin θ)$ （其中 $r \geq 0$ ， $θ \in R$ ）的形式，通常称之为复数z的三角形式．法国数学家棣莫弗发现： $[r {(\cos θ + i \sin θ]}^{n} = r^{n} \cos n θ + i \sin n θ, (n \in N_{+})$ ，我们称这个结论为棣莫弗定理．由棣莫弗定理可知，“ $n$ 为偶数”是“复数 ${(\cos \frac{π}{4} + i \sin \frac{π}{4})}^{m}$ 为纯虚数的是（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 已知点 $A$ ， $B$ ， $C$ 均在半径为 $\sqrt{2}$ 的圆上，若 $| A B | = 2$ ，则 $\vec{A C} \cdot \vec{B C}$ 的最大值为（）

A、 $3 + 2 \sqrt{2}$ B、 $2 + 2 \sqrt{2}$ C、4 D、 $\sqrt{2}$

查看试题解析
8. 在三棱锥 $P - A B C$ 中， $A B = 2$ ， $A C ⊥ B C$ ，若该三棱锥的体积为 $\frac{2}{3}$ ，则其外接球表面积的最小值为（）

A、 $5 π$ B、 $\frac{49 π}{12}$ C、 $\frac{64 π}{9}$ D、 $\frac{25 π}{4}$

查看试题解析

二、多选题

9. 已知在某市的一次学情检测中，学生的数学成绩 $X$ 服从正态分布 $N (100, 100)$ ，其中90分为及格线，120分为优秀线．下列说法正确的是（）．
附：随机变量 $ξ$ 服从正态分布 $N (u, σ^{2})$ ，则 $P (μ - σ < ξ < u + σ) = 0.6826$ ， $P (μ - 2 σ < ξ < μ + 2 σ) = 0.9544$ ， $P (u - 3 σ < ξ < μ + 3 σ) = 0.9974$

A、该市学生数学成绩的期望为100 B、该市学生数学成绩的标准差为100 C、该市学生数学成绩及格率超过0.8 D、该市学生数学成绩不及格的人数和优秀的人数大致相等

查看试题解析
10. 已知圆锥的顶点为 $P$ ，母线长为2，底面半径为 $\sqrt{3}$ ，A，B为底面圆周上两个动点，则下列说法正确的是（）

A、圆锥的高为1 B、三角形 $P A B$ 为等腰三角形 C、三角形 $P A B$ 面积的最大值为 $\sqrt{3}$ D、直线 $P A$ 与圆锥底面所成角的大小为 $\frac{π}{6}$

查看试题解析
11. 已知实数x，y，z满足 $\ln x = e^{y} = \frac{1}{z}$ ，则下列关系式中可能成立的是（）

A、 $x > y > z$ B、 $x > z > y$ C、 $z > x > y$ D、 $z > y > x$

查看试题解析
12. 已知函数 $f (x) = \sin (ω x + φ)$ （其中， $ω > 0$ ， $| φ | < \frac{π}{2}$ ）， $f (- \frac{π}{8}) = 0$ ， $f (x) \leq | f (\frac{3 π}{8}) |$ 恒成立，且 $f (x)$ 在区间 $(- \frac{π}{12}, \frac{π}{24})$ 上单调，则下列说法正确的是（）

A、存在 $φ$ ，使得 $f (x)$ 是偶函数 B、 $f (0) = f (\frac{3 π}{4})$ C、 $ω$ 是奇数 D、 $ω$ 的最大值为3

查看试题解析

三、填空题

13. 5G指的是第五代移动通信技术，比第四代移动通信技术的数据传输速率快数百倍，某公司在研发5G项目时遇到一项技术难题，由甲、乙两个部门分别独立攻关，已知甲部门攻克该技术难题的概率为0.6，乙部门攻克该技术难题的概率为0.5．则该公司攻克这项技术难题的概率为．

查看试题解析
14. 能够说明“若 $\frac{1}{a} > \frac{1}{b}$ ，则 $a < b$ ”是假命题的一组整数a，b的值依次为．

查看试题解析
15. 已知函数 $f (x) = e^{x} - a (x + 1)$ ，若 $f (x)$ 有两个零点，则实数 $a$ 的取值范围是．

查看试题解析
16. 已知 $F_{1}$ ， $F_{2}$ 分别是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左，右焦点，过点 $F_{1}$ 向一条渐近线作垂线，交双曲线右支于点 $P$ ，直线 $F_{2} P$ 与 $y$ 轴交于点Q（P，Q在x轴同侧），连接 $Q F_{1}$ ，若 $△ P Q F_{1}$ 的内切圆圆心恰好落在以 $F_{1} F_{2}$ 为直径的圆上，则 $∠ F_{1} P F_{2}$ 的大小为；双曲线的离心率为．

查看试题解析

四、解答题

17. 2020年4月21日，习近平总书记到安康市平利县老县镇考察调研，在镇中心小学的课堂上向孩子们发出了“文明其精神，野蛮其体魄”的期许某市教育部门为了了解全市01中学生疫情期间居家体育锻炼的情况，从全市随机抽1000名中学生进行调查，统计他们每周参加体育锻炼的时长，右图是根据调查结果绘制的频率分布直方图．

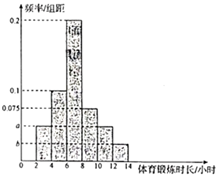(1)、已知样本中每周体育锻炼时长不足4小时的体育锻炼的中学生有100人，求直方图中a，b的值；

(2)、为了更具体地了解全市中学生疫情期间的体育锻炼情况，利用分层抽样的方法从 $[10 ， 12)$ 和 $[12 ， 14]$ 两组中共抽取了6名中学生参加线上座谈会，现从上述6名学生中随机抽取2名在会上进行体育锻炼视频展示，求这2名学生来自不同组的概率．

查看试题解析
18. 已知 $△ A B C$ 中，三个内角A，B，C所对的边分别是a，b，c．

(1)、证明： $a \cos B + b \cos A = c$ ；

(2)、在① $\frac{2 c - b}{\cos B} = \frac{a}{\cos A}$ ，② $c \cos A = 2 b \cos A - a \cos C$ ，③ $2 a - \frac{b \cos C}{\cos A} = \frac{c \cos B}{o s A}$ 这三个条件中任选一个补充在下面问题中，并解答
若 $a = 7$ ， $b = 5$ ，__________，求 $△ A B C$ 的周长．

查看试题解析
19. 如图，三棱锥 $P - A B C$ 中，平面 $P A B ⊥$ 平面 $A B C$ ， $∠ P A B = ∠ P B A = 45^{°}$ ， $∠ A B C = 2 ∠ B A C = 60^{°}$ ， $D$ 是棱 $A B$ 的中点，点 $E$ 在棱 $P B$ 上点 $G$ 是 $△ B C D$ 的重心．

(1)、若E是 $P B$ 的中点，证明 $G E / /$ 面 $P A C$ ；

(2)、是否存在点E，使二面角 $E - C D - G$ 的大小为 $30^{°}$ ，若存在，求 $\frac{B E}{B P}$ 的值；若不存在，请说明理由．

查看试题解析
20. 如图1，杨辉三角是我国南宋数学家杨辉于1261年所著的《详解九章算法》中列出的一张图表，如图2，把杨辉三角左对齐排列，将同一条斜线上的数字求和，会得到一个数列 ${a_{n}}$ ，其中 $a_{1} = 1$ ， $a_{2} = 1$ ， $a_{3} = 2$ …设数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ．

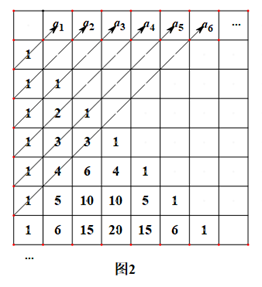(1)、求 $a_{8}$ 的值，并写 $a_{n}$ ， $a_{n}_{+ 1}$ ， $a_{n + 2}$ 出满足的递推关系式（不用证明）；

(2)、记 $a_{2022} = m$ ，用 $m$ 表示 $S_{2020}$ ．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点和下顶点分别为A，B， $| A B | = 2 \sqrt{5}$ ，过椭圆焦点且与长轴垂直的弦的长为2．

(1)、求椭圆C的方程；

(2)、已知M为椭圆C上一动点（M不与A，B重合），直线 $A M$ 与y轴交于点P，直线 $B M$ 与x轴交于点Q，证明： $| A Q | \cdot | B P |$ 为定值．

查看试题解析
22. 已知函数 $f (x) = \frac{\ln x}{e^{a x}}$ 存在唯一的极值点 $x_{0}$ ．

(1)、求实数a的取值范围；

(2)、若 $x_{1} ， x_{2} \in (x_{0} ， + \infty)$ ，证明： $\log_{(x_{1} + x_{2})} (x_{1} + x_{2} ） > e^{- a x_{1}} + e^{- a x_{2}}$ ．

查看试题解析