山东省滨州市2020届高三数学二模试卷
试卷更新日期:2020-07-03 类型:高考模拟
一、单选题
-
1. 已知角 的终边经过点 ,则 ( )A、 B、 C、 D、2. 已知集合 ,则 ( )A、 B、 C、 D、3. 设复数z满足 ,z在复平面内对应的点为 ,则( )A、 B、 C、 D、4. 设 , , ,则a,b,c的大小关系是( )A、 B、 C、 D、5. 已知正方形 的边长为 ( )A、3 B、-3 C、6 D、-66. 函数y= 的图象大致是( )A、
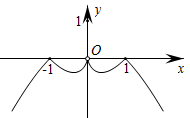
B、
B、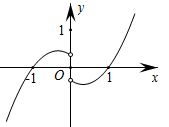
C、
C、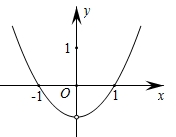
D、
D、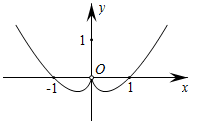
7. 已知O,A,B,C为平面 内的四点,其中A,B,C三点共线,点O在直线 外,且满足 .其中 ,则 的最小值为( )A、21 B、25 C、27 D、348. 我国南北朝时期的数学家祖暅提出了一条原理:“幂势既同,则积不容异”即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.椭球是椭圆绕其长轴旋转所成的旋转体,如图,将底面半径都为 .高都为 的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面 上,用平行于平面 且与平面 任意距离d处的平面截这两个几何体,截面分别为圆面和圆环,可以证明 圆= 圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )
7. 已知O,A,B,C为平面 内的四点,其中A,B,C三点共线,点O在直线 外,且满足 .其中 ,则 的最小值为( )A、21 B、25 C、27 D、348. 我国南北朝时期的数学家祖暅提出了一条原理:“幂势既同,则积不容异”即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.椭球是椭圆绕其长轴旋转所成的旋转体,如图,将底面半径都为 .高都为 的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面 上,用平行于平面 且与平面 任意距离d处的平面截这两个几何体,截面分别为圆面和圆环,可以证明 圆= 圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )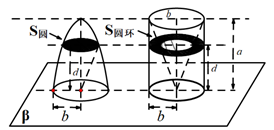 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中错误的是( )
 A、消耗1升汽油乙车最多可行驶5千米. B、以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多. C、甲车以80千米/小时的速度行驶1小时,消耗10升汽油. D、某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油.10. 设 , 分别为双曲线 的左、右焦点,若在双曲线右支上存在点 ,满足 ,且 到直线 的距离等于双曲线的实轴长,则关于该双曲线的下列结论正确的是( )A、渐近线方程为 B、渐近线方程为 C、离心率为 D、离心率为11. 已知函数 的图象的一条对称轴为 ,则下列结论中正确的是( )A、 是最小正周期为 的奇函数 B、 是 图像的一个对称中心 C、 在 上单调递增 D、先将函数 图象上各点的纵坐标缩短为原来的 ,然后把所得函数图象再向左平移 个单位长度,即可得到函数 的图象.12. 如图,点M是正方体 中的侧面 上的一个动点,则下列结论正确的是( )
A、消耗1升汽油乙车最多可行驶5千米. B、以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多. C、甲车以80千米/小时的速度行驶1小时,消耗10升汽油. D、某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油.10. 设 , 分别为双曲线 的左、右焦点,若在双曲线右支上存在点 ,满足 ,且 到直线 的距离等于双曲线的实轴长,则关于该双曲线的下列结论正确的是( )A、渐近线方程为 B、渐近线方程为 C、离心率为 D、离心率为11. 已知函数 的图象的一条对称轴为 ,则下列结论中正确的是( )A、 是最小正周期为 的奇函数 B、 是 图像的一个对称中心 C、 在 上单调递增 D、先将函数 图象上各点的纵坐标缩短为原来的 ,然后把所得函数图象再向左平移 个单位长度,即可得到函数 的图象.12. 如图,点M是正方体 中的侧面 上的一个动点,则下列结论正确的是( ) A、点M存在无数个位置满足 B、若正方体的棱长为1,三棱锥 的体积最大值为 C、在线段 上存在点M,使异面直线 与 所成的角是 D、点M存在无数个位置满足到直线 和直线 的距离相等.
A、点M存在无数个位置满足 B、若正方体的棱长为1,三棱锥 的体积最大值为 C、在线段 上存在点M,使异面直线 与 所成的角是 D、点M存在无数个位置满足到直线 和直线 的距离相等.三、填空题
-
13. 古典著作《连山易》中记载了金、木、水、火土之间相生相克的关系,如图所示,现从五种不同属性的物质中任取两种,则取出的两种物质恰是相克关系的概率为
 14. 已知点A,B,C,D均在球O的球面上, , ,若三棱锥 体积的最大值是 ,则球O的表面积为15. 设 是定义在R上且周期为6的周期函数,若函数 的图象关于点 对称,函数 在区间 (其中 )上的零点的个数的最小值为 ,则
14. 已知点A,B,C,D均在球O的球面上, , ,若三棱锥 体积的最大值是 ,则球O的表面积为15. 设 是定义在R上且周期为6的周期函数,若函数 的图象关于点 对称,函数 在区间 (其中 )上的零点的个数的最小值为 ,则四、双空题
-
16. 动圆E与圆 外切,并与直线 相切,则动圆圆心E的轨迹方程为 , 过点 作倾斜角互补的两条直线,分别与圆心E的轨迹相交于A,B两点,则直线 的斜率为.
五、解答题
-
17. 已知△ 的内角A,B,C的对边分别为a,b,c,若 ,________,求△ 的周长L和面积S.
在① , ,② , ,③ , 这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
18. 已知 为等差数列, , , 为等比数列,且 , .(1)、求 , 的通项公式;(2)、记 ,求数列 的前n项和 .19. 如图所示,在等腰梯形 中, ∥ , ,直角梯形 所在的平面垂直于平面 ,且 , . (1)、证明:平面 平面 ;(2)、点 在线段 上,试确定点 的位置,使平面 与平面 所成的二面角的余弦值为 .20. 已知椭圆 经过点 ,离心率为(1)、求椭圆C的方程;(2)、设直线 与椭圆C相交于A,B两点,若以 , 为邻边的平行四边形 的顶点P在椭圆C上,求证:平行四边形 的面积为定值.21. 在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
(1)、证明:平面 平面 ;(2)、点 在线段 上,试确定点 的位置,使平面 与平面 所成的二面角的余弦值为 .20. 已知椭圆 经过点 ,离心率为(1)、求椭圆C的方程;(2)、设直线 与椭圆C相交于A,B两点,若以 , 为邻边的平行四边形 的顶点P在椭圆C上,求证:平行四边形 的面积为定值.21. 在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:潜伏期(单位:天)
人数
17
41
62
50
26
3
1
附:
0.05
0.025
0.010
3.841
5.024
6.635
,其中
(1)、求这200名患者的潜伏期的样本平均数 (同一组中的数据用该组区间的中点值作代表);(2)、该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述200名患者中抽取40人得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;潜伏期 天
潜伏期 天
总计
50岁以上(含50岁)
20
50岁以下
9
总计
40
(3)、以这200名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入硏究,该研究团队在该地区随机调查了10名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?22. 已知函数 ,(1)、讨论函数 的单调性;(2)、当 时,证明曲线 分别在点 和点 处的切线为不同的直线;(3)、已知过点 能作曲线 的三条切线,求m,n所满足的条件.
-