河北省2016年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题
-
1. 计算:-(-1)=( )A、±1 B、-2 C、-1 D、12. 计算正确的是( )A、(-5)0=0 B、x2+x3=x5 C、(ab2)3=a2b5 D、2a2·a-1=2a3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、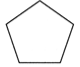 C、
C、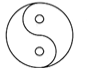 D、
D、 4. 下列运算结果为x-1的是( )A、 B、 C、 D、5. 若k≠0,b<0,则y=kx+b的图象可能是( )A、
4. 下列运算结果为x-1的是( )A、 B、 C、 D、5. 若k≠0,b<0,则y=kx+b的图象可能是( )A、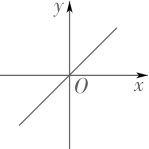 B、
B、 C、
C、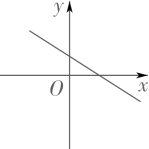 D、
D、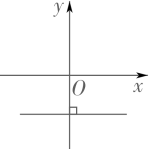 6. 关于▱ABCD的叙述,正确的是( )A、若AB⊥BC,则▱ABCD是菱形 B、若AC⊥BD,则▱ABCD是正方形 C、若AC=BD,则▱ABCD是矩形 D、若AB=AD,则▱ABCD是正方形7. 关于 的叙述,错误的是( )A、 是有理数 B、面积为12的正方形边长是 C、 =2 D、在数轴上可以找到表示 的点8. 图1和图2中所有的正方形都全等,将图1的正方形放在图2中的 1 2 3 4 某一位置,所组成的图形不能围成正方体的位置是( )
6. 关于▱ABCD的叙述,正确的是( )A、若AB⊥BC,则▱ABCD是菱形 B、若AC⊥BD,则▱ABCD是正方形 C、若AC=BD,则▱ABCD是矩形 D、若AB=AD,则▱ABCD是正方形7. 关于 的叙述,错误的是( )A、 是有理数 B、面积为12的正方形边长是 C、 =2 D、在数轴上可以找到表示 的点8. 图1和图2中所有的正方形都全等,将图1的正方形放在图2中的 1 2 3 4 某一位置,所组成的图形不能围成正方体的位置是( )
图1 图2
A、1 B、2 C、3 D、49. 图示为4×4的网格图,A , B , C , D , O均在格点上,点O是( ) A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心10. 如图,已知钝角△ABC , 依下列步骤尺规作图,并保留作图痕迹.
A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心10. 如图,已知钝角△ABC , 依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧 1 ;
步骤2:以B为圆心,BA为半径画弧 2 ,将弧 1 于点D;
步骤3:连接AD , 交BC延长线于点H.
下列叙述正确的是( )
 A、BH垂直分分线段AD B、AC平分∠BAD C、S△ABC=BC·AH D、AB=AD11. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b。对于以下结论:
A、BH垂直分分线段AD B、AC平分∠BAD C、S△ABC=BC·AH D、AB=AD11. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b。对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁: >0 。其中正确的是( )
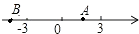 A、甲、乙 B、丙、丁 C、甲、丙 D、乙、丁12. 在求3x的倒数的值时,嘉淇同学将3x看成了8x , 她求得的值比符合题意答案小5.依上述情形,所列关系式成立的是( )A、 B、 C、 D、13. 如图,将 ABCD沿对角线AC折叠,使点B落在点B’处.若∠1=∠2=44°,则∠B为( )
A、甲、乙 B、丙、丁 C、甲、丙 D、乙、丁12. 在求3x的倒数的值时,嘉淇同学将3x看成了8x , 她求得的值比符合题意答案小5.依上述情形,所列关系式成立的是( )A、 B、 C、 D、13. 如图,将 ABCD沿对角线AC折叠,使点B落在点B’处.若∠1=∠2=44°,则∠B为( )
第13题图
A、66° B、104° C、114° D、124°14. a,b,c为常数,且(a-c)2>a2+c2 , 则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为015. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( ) A、
A、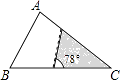 B、
B、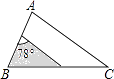 C、
C、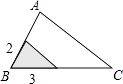 D、
D、 16. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
16. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )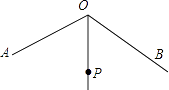 A、1个 B、2个 C、3个 D、3个以上
A、1个 B、2个 C、3个 D、3个以上二、填空题
-
17. 8的立方根为.18. 若mn=m+3,则2mn+3m-5nm+10=.19. 如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.

当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2 , 易知∠1=∠2.若A1A2⊥AO , 光线又会沿A2→A1→A原路返回到点A,此时∠A=°.
若光线从点A发出后,经若干次反射能沿原路返回到点A , 则锐角∠A的最小值=°.
三、解答题
-
20.

请你参考黑板中老师的讲解,用运算律简便计算:
(1)、999×(-15);(2)、999× +999×( )-999× .21. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.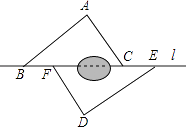 (1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.22. 已知n边形的内角和θ=(n-2)×180°.(1)、甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)、若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.23. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.
(1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.22. 已知n边形的内角和θ=(n-2)×180°.(1)、甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)、若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.23. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.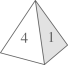 图1
图1  图2
图2如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从图A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;……
设游戏者从圈A起跳.
(1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?24. 某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价x(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)、求y与x的函数关系式,并确定x的取值范围;(2)、某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?(3)、这n个玩具调整前、后的平均单价分别为 , ,猜想 与 的关系式,并写出推导出过.25. 如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M , 其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.发现 AP(弧)的长与QB(弧)的长之和为定值l , 求l;
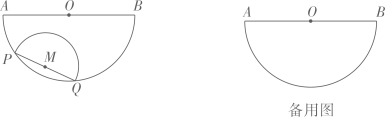 (1)、【思考】
(1)、【思考】点M与AB的最大距离为 , 此时点P , A间的距离为;点M与AB的最小距离为 , 此时半圆M的弧与AB所围成的封闭图形面积为.
(2)、【探究】当半圆M与AB相切时,求AP(弧)的长.
(注:结果保留π,cos 35°= ,cos 55°= )
26. 如图,抛物线L: (常数t>0)与x轴从左到右的交点为B , A , 过线段OA的中点M作MP⊥x轴,交双曲线 于点P , 且OA·MP=12.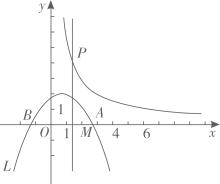 (1)、求k值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G , 用t表示图象G最高点的坐标;(4)、设L与双曲线有个交点的横坐标为x0 , 且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
(1)、求k值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G , 用t表示图象G最高点的坐标;(4)、设L与双曲线有个交点的横坐标为x0 , 且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.