河北省2015年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题
-
1. 计算:3﹣2×(﹣1)=( )A、5 B、1 C、﹣1 D、62. 下列说法正确的是( )A、1的相反数是﹣1 B、1的倒数是﹣1 C、1的立方根是±1 D、﹣1是无理数3.
一张菱形纸片按如图1、图2依次对折后,再按如图3打出一个圆形小孔,则展开铺平后的图案是( )
 A、
A、 B、
B、 C、
C、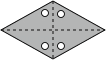 D、
D、 4. 下列运算正确的是( )A、( )﹣1=﹣ B、6×107=6000000 C、(2a)2=2a2 D、a3•a2=a55. 如图所示的三视图所对应的几何体是( )
4. 下列运算正确的是( )A、( )﹣1=﹣ B、6×107=6000000 C、(2a)2=2a2 D、a3•a2=a55. 如图所示的三视图所对应的几何体是( ) A、
A、 B、
B、 C、
C、 D、
D、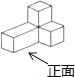 6. 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
6. 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( ) A、△ABE B、△ACF C、△ABD D、△ADE7.
A、△ABE B、△ACF C、△ABD D、△ADE7.在数轴上标注了四段范围,如图,则表示的点落在( )
 A、段① B、段② C、段③ D、段④8. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A、段① B、段② C、段③ D、段④8. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )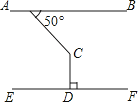 A、120° B、130° C、140° D、150°9. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )A、
A、120° B、130° C、140° D、150°9. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )A、 B、
B、 C、
C、 D、
D、 10. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20 . 则y与x的函数图象大致是( )
10. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20 . 则y与x的函数图象大致是( )
A、 B、
B、 C、
C、  D、
D、 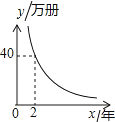 11. 利用加减消元法解方程组 ,下列做法正确的是( )A、要消去y,可以将①×5+②×2 B、要消去x,可以将①×3+②×(﹣5) C、要消去y,可以将①×5+②×3 D、要消去x,可以将①×(﹣5)+②×212. 若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( ).A、a<1 B、a>1 C、a≤1 D、a≥113. 将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是( )A、 B、 C、 D、14. 如图,直线l:y=﹣ x﹣3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
11. 利用加减消元法解方程组 ,下列做法正确的是( )A、要消去y,可以将①×5+②×2 B、要消去x,可以将①×3+②×(﹣5) C、要消去y,可以将①×5+②×3 D、要消去x,可以将①×(﹣5)+②×212. 若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( ).A、a<1 B、a>1 C、a≤1 D、a≥113. 将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是( )A、 B、 C、 D、14. 如图,直线l:y=﹣ x﹣3与直线y=a(a为常数)的交点在第四象限,则a可能在( ) A、1<a<2 B、﹣2<a<0 C、﹣3≤a≤﹣2 D、﹣10<a<﹣415. 如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
A、1<a<2 B、﹣2<a<0 C、﹣3≤a≤﹣2 D、﹣10<a<﹣415. 如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值: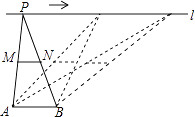
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A、②③ B、②⑤ C、①③④ D、④⑤16.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以
A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以二、填空题
-
17. 若|a|=20150 , 则a= .18. 若a=2b≠0,则 的值为 .
19.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2= .
 20.
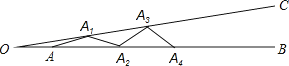
20.如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n= .
三、解答题
-
21.
老师在黑板上书写了一个正确的演算过程随后用手掌捂住了如图所示的一个二次三项式,形式如图:
 (1)、求所捂的二次三项式;(2)、若x=+1,求所捂二次三项式的值.22. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
(1)、求所捂的二次三项式;(2)、若x=+1,求所捂二次三项式的值.22. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证. (1)、在方框中填空,以补全已知和求证;
(1)、在方框中填空,以补全已知和求证;已知:如图1,在四边形ABCD中,BC=AD,AB=
求证:四边形ABCD是四边形.
(2)、按嘉淇的想法写出证明;(3)、用文字叙述所证命题的逆命题为 .23.水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.
 (1)、只放入大球,且个数为x大 , 求y与x大的函数关系式(不必写出x大的范围);(2)、仅放入6个大球后,开始放入小球,且小球个数为x小
(1)、只放入大球,且个数为x大 , 求y与x大的函数关系式(不必写出x大的范围);(2)、仅放入6个大球后,开始放入小球,且小球个数为x小①求y与x小的函数关系式(不必写出x小范围);
②限定水面高不超过260毫米,最多能放入几个小球?
24. 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如表统计表及不完整的折线图.A,B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
并求得了A产品三次单价的平均数和方差:
=5.9,sA2= [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
 (1)、补全如图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了%(2)、求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)、该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.25.
(1)、补全如图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了%(2)、求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)、该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.25.如图,已知点O(0,0),A(﹣5,0),B(2,1),抛物线l:y=﹣(x﹣h)2+1(h为常数)与y轴的交点为C.
 (1)、l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标;
(1)、l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标;
(2)、设点C的纵坐标为yc , 求yc的最大值,此时l上有两点(x1 , y1),(x2 , y2),其中x1>x2≥0,比较y1与y2的大小;
(3)、当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.26. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=0D=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).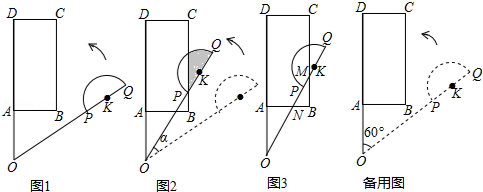
发现:
(1)、当α=0°,即初始位置时,点P直线AB上.(填“在”或“不在”)求当α是多少时,OQ经过点B.(2)、在OQ旋转过程中,简要说明α是多少时,点P,A间的距离最小?并指出这个最小值;(3)、如图2,当点P恰好落在BC边上时,求a及S阴影(4)、如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.(5)、当半圆K与矩形ABCD的边相切时,求sinα的值.