新疆生产建设兵团2020年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、单项选择题(本大题共9小题,每小题5分,共45分.)
-
1. 下列各数中,是负数的为( )A、-1 B、0 C、0.2 D、2. 如图所示,该几何体的俯视图是( )
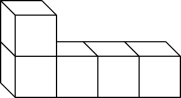 A、
A、 B、
B、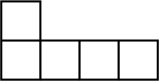 C、
C、 D、
D、 3. 下列运算正确的是( )A、x2·x3=x6 B、x6÷x3=x3 C、x3+x3=2x6 D、(-2x)3=-6x34. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
3. 下列运算正确的是( )A、x2·x3=x6 B、x6÷x3=x3 C、x3+x3=2x6 D、(-2x)3=-6x34. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( ) A、a>b B、|a|>|b| C、-a<b D、a+b>05. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、x2+2x+4=0 C、x2-x+2=0 D、x2-2x=06. 不等式组 的解集是( )A、0<x≤2 B、0<x≤6 C、x>0 D、x≤27. 四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )
A、a>b B、|a|>|b| C、-a<b D、a+b>05. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、x2+2x+4=0 C、x2-x+2=0 D、x2-2x=06. 不等式组 的解集是( )A、0<x≤2 B、0<x≤6 C、x>0 D、x≤27. 四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )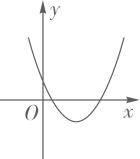 A、
A、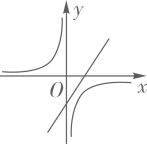 B、
B、 C、
C、 D、
D、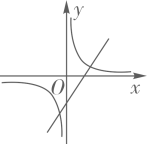 9. 如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为( )
9. 如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为( )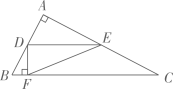 A、 B、5 C、4 D、10
A、 B、5 C、4 D、10二、填空题(本大题共6小题,每小题5分,共30分)
-
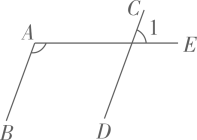
10. 如图,若AB∥CD,∠A=110°,则∠1=°.
 11. 分解因式:am2-an2=.12. 表中记录了某种苹果树苗在一定条件下移植成活的情况:
11. 分解因式:am2-an2=.12. 表中记录了某种苹果树苗在一定条件下移植成活的情况:移植的棵数n
200
500
800
2000
12000
成活的棵数m
187
446
730
1790
10836
成活的频率
0.935
0.892
0.913
0.895
0.903
由此估计这种苹果树苗移植成活的概率约为.(精确到0.1)
13. 如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为. 14. 如图,⊙O的半径是2,扇形BAC的圆心角为60°.若将扇形BAC剪下围成一个圆锥,则此圆锥的底面圆的半径为.
14. 如图,⊙O的半径是2,扇形BAC的圆心角为60°.若将扇形BAC剪下围成一个圆锥,则此圆锥的底面圆的半径为. 15. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.
15. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.
三、解答题(本大题共8小题,共75分)
-
16. 计算: .17. 先化简,再求值:(x-2)2-4x(x-1)+(2x+1)(2x-1),其中x=- .18. 如图,四边形ABCD是平行四边形,DE∥BF,且分别交对角线AC于点E,F,连接BE,DF.
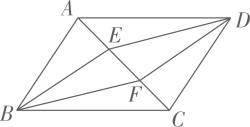 (1)、求证:AE=CF;(2)、若BE=DE,求证:四边形EBFD为菱形.19. 为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩(x)分为四个等级:优秀85≤x≤100;良好75≤x<85;及格60≤x<75;不及格0≤x<60,并绘制成如图两幅统计图.
(1)、求证:AE=CF;(2)、若BE=DE,求证:四边形EBFD为菱形.19. 为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩(x)分为四个等级:优秀85≤x≤100;良好75≤x<85;及格60≤x<75;不及格0≤x<60,并绘制成如图两幅统计图.
根据以上信息,解答下列问题:
(1)、在抽取的学生中不及格人数所占的百分比是;(2)、计算所抽取学生测试成绩的平均分;(3)、若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.20. 如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为58°(A,B,C三点在一条直线上),求建筑物CD的高度.(结果保留整数.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)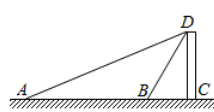 21. 某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A、B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?22. 如图,在⊙O中,AB为⊙O的直径,C为⊙O上一点,P是 的中点,过点P作AC的垂线,交AC的延长线于点D.
21. 某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A、B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?22. 如图,在⊙O中,AB为⊙O的直径,C为⊙O上一点,P是 的中点,过点P作AC的垂线,交AC的延长线于点D.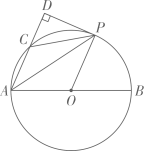 (1)、求证:DP是⊙O的切线;(2)、若AC=5,sin∠APC= ,求AP的长.23. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c的顶点是A(1,3),将OA绕点O顺时针旋转90°后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
(1)、求证:DP是⊙O的切线;(2)、若AC=5,sin∠APC= ,求AP的长.23. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c的顶点是A(1,3),将OA绕点O顺时针旋转90°后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.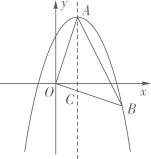 (1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与△OAB的边分别交于M,N两点,将△AMN以直线MN为对称轴翻折,得到△A′MN,设点P的纵坐标为m.
(1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与△OAB的边分别交于M,N两点,将△AMN以直线MN为对称轴翻折,得到△A′MN,设点P的纵坐标为m.①当△A′MN在△OAB内部时,求m的取值范围;
②是否存在点P,使S△A′MN= S△OA′B , 若存在,求出满足条件m的值;若不存在,请说明理由.