天津市2015年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题
-
1. 计算(﹣18)÷6的结果等于( )A、﹣3 B、3 C、﹣ D、2. cos45°的值等于( )A、 B、 C、 D、3. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 据2015年5月4日《天津日报》报道,“五一”三天假期,全市共接待海内外游客约2270000人次.将2270000用科学记数法表示应为( )A、0.227×107 B、2.27×106 C、22.7×105 D、227×1045.
4. 据2015年5月4日《天津日报》报道,“五一”三天假期,全市共接待海内外游客约2270000人次.将2270000用科学记数法表示应为( )A、0.227×107 B、2.27×106 C、22.7×105 D、227×1045.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
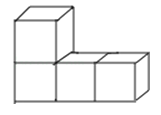 A、
A、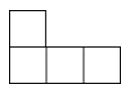 B、
B、 C、
C、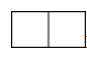 D、
D、 6. 估计的值在( )
6. 估计的值在( )
A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间7. 在平面直角坐标系中,把点P(﹣3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )A、(3,2) B、(2,﹣3) C、(﹣3,﹣2) D、(3,﹣2)8. 分式方程 = 的解为( )A、x=0 B、x=5 C、x=3 D、x=99. 已知反比例函数 , 当1<x<3时,y的取值范围是( )
A、0<y<l B、1<y<2 C、2<y<6 D、y>610. 已知一个表面积为12dm2的正方体,则这个正方体的棱长为( )
A、1dm B、dm C、dm D、3dm11.如图,已知▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
 A、130° B、150° C、160° D、170°12. 已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )A、 B、 C、 D、
A、130° B、150° C、160° D、170°12. 已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )A、 B、 C、 D、二、填空题
-
13. 计算:x2•x5的结果等于 .
14. 若一次函数y=2x+b(b为常数)的图象经过点(1,5),则b的值为 .
15. 不透明袋子中装有9个球,其中有2个红球、3个绿球和4个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为 .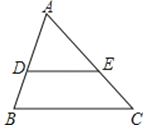 17.
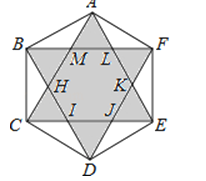
17.如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有 个.
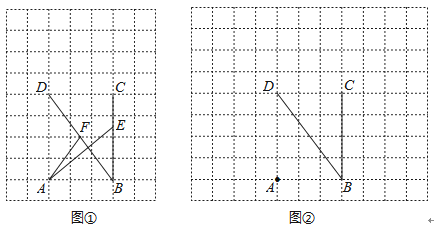
 18. 在每个小正方形的边长为1的网格中.点A,B,D均在格点上,点E、F分别为线段BC、DB上的动点,且BE=DF.
18. 在每个小正方形的边长为1的网格中.点A,B,D均在格点上,点E、F分别为线段BC、DB上的动点,且BE=DF.(Ⅰ)如图①,当BE=时,计算AE+AF的值等于
(Ⅱ)当AE+AF取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE,AF,并简要说明点E和点F的位置如何找到的(不要求证明)
三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、不等式①,得;(2)、不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来 (4)、原不等式组的解集为 .20. 某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题.
(4)、原不等式组的解集为 .20. 某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题. (1)、该商场服装部营业员的人数为 ,图①中m的值为(2)、求统计的这组销售额额数据的平均数、众数和中位数.21. 已知A、B、C是⊙O上的三个点.四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(1)、该商场服装部营业员的人数为 ,图①中m的值为(2)、求统计的这组销售额额数据的平均数、众数和中位数.21. 已知A、B、C是⊙O上的三个点.四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.(Ⅰ)如图①,求∠ADC的大小.
(Ⅱ)如图②,经过点O作CD的平行线,与AB交于点E , 与 交于点F , 连接AF , 求∠FAB的大小.
 22. 如图,某建筑物BC顶部有釕一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
22. 如图,某建筑物BC顶部有釕一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.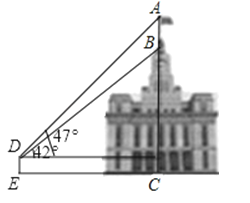 23. 1号探测气球从海拔5m处出发,以lm/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都匀速上升了50min.
23. 1号探测气球从海拔5m处出发,以lm/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都匀速上升了50min.设气球球上升时间为xmin (0≤x≤50)
(1)、根据题意,填写下表:上升时间/min
10
30
…
x
1号探测气球所在位置的海拔/m
15
35
…
x+5
2号探测气球所在位置的海拔/m
20
30
…
0.5x+15
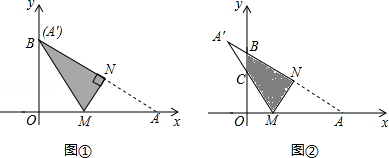
(2)、在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由(3)、当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?24. 将一个直角三角形纸片ABO , 放置在平面直角坐标系中,点A( ,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O , A重合)作MN丄AB于点N , 沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m , 折叠后的△AM′N与四边形OMNB重叠部分的面积为S .(Ⅰ)如图①,当点A′与顶点B重合时,求点M的坐标;
(Ⅱ)如图②,当点A′,落在第二象限时,A′M与OB相交于点C , 试用含m的式子表示S;
(Ⅲ)当S= 时,求点M的坐标(直接写出结果即可).
 25. 已知二次函数y=x2+bx+c(b , c为常数).
25. 已知二次函数y=x2+bx+c(b , c为常数).(Ⅰ)当b=2,c=﹣3时,求二次函数的最小值;
(Ⅱ)当c=5时,若在函数值y=l的怙况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.