贵州省遵义市2020年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题(共12小题).
-
1. ﹣3的绝对值是( )A、3 B、﹣3 C、 D、±32. 在文化旅游大融合的背景下,享受文化成为旅游业的新趋势.今年“五一”假期,我市为游客和市民提供了丰富多彩的文化享受,各艺术表演馆美术馆、公共图书馆、群众文化机构、非遗机构及文物机构累计接待游客18.25万人次,将18.25万用科学记数法表示为( )A、1.825×105 B、1.825×106 C、1.825×107 D、1.825×1083. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
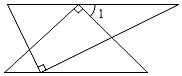 A、30° B、45° C、55° D、60°4. 下列计算正确的是( )A、x2+x=x3 B、(﹣3x)2=6x2 C、8x4÷2x2=4x2 D、(x﹣2y)(x+2y)=x2﹣2y25. 某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )A、众数是36.5 B、中位数是36.7 C、平均数是36.6 D、方差是0.46. 已知x1 , x2是方程x2﹣3x﹣2=0的两根,则x12+x22的值为( )A、5 B、10 C、11 D、137. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )
A、30° B、45° C、55° D、60°4. 下列计算正确的是( )A、x2+x=x3 B、(﹣3x)2=6x2 C、8x4÷2x2=4x2 D、(x﹣2y)(x+2y)=x2﹣2y25. 某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )A、众数是36.5 B、中位数是36.7 C、平均数是36.6 D、方差是0.46. 已知x1 , x2是方程x2﹣3x﹣2=0的两根,则x12+x22的值为( )A、5 B、10 C、11 D、137. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )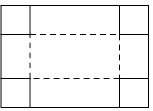 A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6008. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6008. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、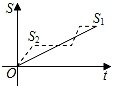 B、
B、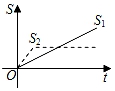 C、
C、 D、
D、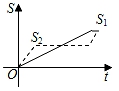 9. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
9. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )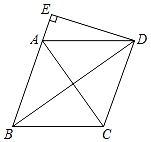 A、 B、 C、4 D、10. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°= = = =2﹣ .类比这种方法,计算tan22.5°的值为( )
A、 B、 C、4 D、10. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°= = = =2﹣ .类比这种方法,计算tan22.5°的值为( )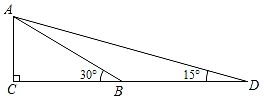 A、 +1 B、 ﹣1 C、 D、11. 如图,△ABO的顶点A在函数y= (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为( )
A、 +1 B、 ﹣1 C、 D、11. 如图,△ABO的顶点A在函数y= (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为( )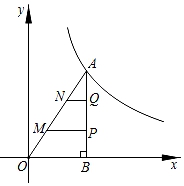 A、9 B、12 C、15 D、1812. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )
A、9 B、12 C、15 D、1812. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本小题共4小题,每小题4分,共16分)
-
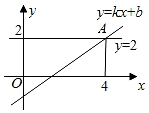
13. 计算: ﹣ 的结果是.14. 如图,直线y=kx+b(k、b是常数k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为.
 15. 如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A′落在MN上.若CD=5,则BE的长是.
15. 如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A′落在MN上.若CD=5,则BE的长是. 16. 如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是.
16. 如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是.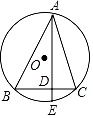
三、解答题(本题共有8小题,共86分.)
-
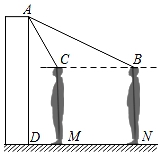
17. 计算:(1)、sin30°﹣(π﹣3.14)0+(﹣ )﹣2;(2)、解方程; = .18. 化简式子 ÷(x﹣ ),从0,1,2中取一个合适的数作为x的值代入求值.19. 某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
 20. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交 于点D,过点D作DE∥BC交AC的延长线于点E.
20. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交 于点D,过点D作DE∥BC交AC的延长线于点E.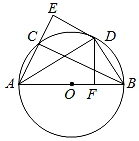 (1)、求证:DE是⊙O的切线;(2)、过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.21. 遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
(1)、求证:DE是⊙O的切线;(2)、过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.21. 遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.课外劳动时间频数分布表
劳动时间分组
频数
频率
0≤t<20
2
0.1
20≤t<40
4
m
40≤t<60
6
0.3
60≤t<80
a
0.25
80≤t<100
3
0.15

解答下列问题:
(1)、频数分布表中a=▲ , m=▲;将频数分布直方图补充完整;(2)、若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;(3)、已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.22. 为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:时间
销售数量(个)
销售收入(元)(销售收入=售价×销售数量)
甲种型号
乙种型号
第一月
22
8
1100
第二月
38
24
2460
(1)、求甲、乙两种型号水杯的售价;(2)、第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.23. 如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.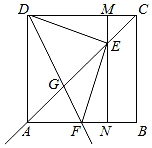 (1)、求证:EF=DE;(2)、当AF=2时,求GE的长.24. 如图,抛物线y=ax2+ x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)、求证:EF=DE;(2)、当AF=2时,求GE的长.24. 如图,抛物线y=ax2+ x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.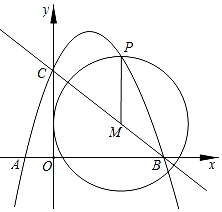 (1)、求该抛物线的解析式;(2)、在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)、以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.
(1)、求该抛物线的解析式;(2)、在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)、以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.