湖北省通城市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（　　）

A、x＜1 B、x≥1 C、x≤﹣1 D、x＜﹣1

查看试题解析
2. 已知正比例函数 $y = kx (k \neq 0)$ 的图象经过点（1，－2），则正比例函数的解析式为（）

A、 $y = 2x$ B、 $y = - 2x$ C、 $y = \frac{1}{2} x$ D、 $y = - \frac{1}{2} x$

查看试题解析
3. 勾股定理是“人类最伟大的十个科学发现之一”.中国对勾股定理的证明最早出现在对《周髀算经》的注解中，它表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲.在《周髀算经》注解中证明勾股定理的是我国古代数学家（）

A、祖冲之 B、杨辉 C、刘徽 D、赵爽

查看试题解析

4. 某品牌鞋店在一个月内销售某款女鞋，各种尺码鞋的销量如下表所示：

尺码/厘米	22.5	23	23.5	24	24.5
销售量/双	35	40	30	17	8

通过分析上述数据，对鞋店业主的进货最有意义的是

A、平均数 B、众数 C、中位数 D、方差

查看试题解析

5. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $2 \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{8} \div \sqrt{2} = 2$

查看试题解析
6. 如图，已知数轴上点 $P$ 表示的数为 $- 1$ ，点 $A$ 表示的数为1，过点 $A$ 作直线 $l$ 垂直于 $P A$ ，在 $l$ 上取点 $B$ ，使 $A B = 1$ ，以点 $P$ 为圆心，以 $P B$ 为半径作弧，弧与数轴的交点 $C$ 所表示的数为（）

A、 $\sqrt{5}$ B、 $\sqrt{5} - 1$ C、 $\sqrt{5} + 1$ D、 $- \sqrt{5} + 1$

查看试题解析
7. 下列命题中，为假命题的是（）

A、两组邻边分别相等的四边形是菱形 B、对角线互相垂直平分的四边形是菱形 C、四个角相等的四边形是矩形 D、对角线相等的平行四边形是矩形

查看试题解析
8. 对于函数 y＝3-x，下列结论正确的是（）

A、y 的值随 x 的增大而增大 B、它的图象必经过点（-1，3） C、它的图象不经过第三象限 D、当 x＞1 时，y＜0.

查看试题解析

二、填空题

9. 化简： $\sqrt{{(- 3)}^{2}}$ = ．

查看试题解析

10. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择.

查看试题解析

11. 写出一个比2大比3小的无理数（用含根号的式子表示）．

查看试题解析
12. 如图，直线l₁：y=x+1与直线l₂：y=kx+b相交于点P(m，3)，则关于x的不等式x+1≤kx+b的解集为.

查看试题解析
13. 菱形ABCD的对角线AC，BD的长分别为6cm，8cm，则这个菱形的周长是cm.

查看试题解析
14. 观察下列各式：3²=4+5，5²=12+13，7²=24+25，9²=40+41…根据发现的规律得到13²= + .

查看试题解析
15. 某市规定了每月用水不超过l8立方米和超过18立方米两种不同的收费标准，该市用户每月应交水费y（元）是用水x（立方米）的函数，其图象如图所示.已知小丽家3月份交了水费102元，则小丽家这个月用水量为立方米.

查看试题解析
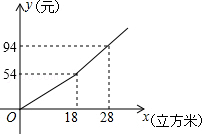16. 如图，在平面直角坐标系xOy中，菱形AOBC的边长为8，∠AOB=60°. 点D是边OB上一动点，点E在BC上，且∠DAE=60°.

有下列结论：

①点C的坐标为（12， $4 \sqrt{3}$ ）；②BD=CE；

③四边形ADBE的面积为定值；

④当D为OB的中点时，△DBE的面积最小.

其中正确的有.（把你认为正确结论的序号都填上）

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{18} - \sqrt{12} + \sqrt{2}$

(2)、（ $\sqrt{5} + 3$ ）（ $\sqrt{5} + 2$ ）

查看试题解析
18. 如图，正方形网格的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上.

(1)、分别求出AB，BC，AC的长；

(2)、试判断△ABC是什么三角形，并说明理由.

查看试题解析
19. 已知一次函数的图象经过点（3，5）与（ $- 4$ ， $- 9$ ）.

(1)、求这个一次函数的解析式；

(2)、点A（2，3）是否在这个函数的图象上，请说明理由.

查看试题解析
20. 某中学八⑴班、⑵班各选5名同学参加“爱我中华”演讲比赛，其预赛成绩（满分100分）如图所示：

(1)、根据上图填写下表：

平均数

中位数

众数

八（1）班

85

85

八（2）班

85

80

(2)、根据两班成绩的平均数和中位数，分析哪班成绩较好？

(3)、如果每班各选2名同学参加决赛，你认为哪个班实力更强些？请说明理由.

查看试题解析
21. 如图，平行四边形ABCD中，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF.

(1)、求证：四边形CEDF为平行四边形；

(2)、若AB＝6cm，BC＝10cm，∠B＝60°，
①当AE＝cm时，四边形CEDF是矩形；

②当AE＝cm时，四边形CEDF是菱形.

查看试题解析
22. “黄金1号”玉米种子的价格为5元/kg.如果一次购买5kg以上的种子，超过5kg部分的种子价格打8折.

(1)、购买3kg种子，需付款元，购买6kg种子，需付款元.

(2)、设购买种子x kg，付款金额为y元，写出y与x之间的函数解析式.

(3)、张大爷要购买种子5千克，李大爷要购买种子4千克，怎样购买让他们花钱最少？他们各应付款多少元？（结果保留整数）

查看试题解析
23. 如图1，已知正方形ABCD的边长为6，E是CD边上一点（不与点C 重合），以CE为边在正方形ABCD的右侧作正方形CEFG，连接BF、BD、FD.

(1)、当点E与点D重合时，△BDF的面积为；当点E为CD的中点时，△BDF的面积为.

(2)、当E是CD边上任意一点（不与点C重合）时，猜想S_△_BDF与S_正方形_ABCD之间的关系，并证明你的猜想；

(3)、如图2，设BF与CD相交于点H，若△DFH的面积为 $\frac{36}{5}$ ，求正方形CEFG的边长.

查看试题解析
24. 如图，A，B是直线y=x+4与坐标轴的交点，直线y=-2x+b过点B，与x轴交于点C.

(1)、求A，B，C三点的坐标；

(2)、点D是折线A—B—C上一动点.
①当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，用直尺和圆规画出点E的位置（保留作图痕迹，不要求写作法和证明），并求E点的坐标.

②是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由

查看试题解析

	平均数	中位数	众数
八（1）班	85		85
八（2）班	85	80