湖北省随州市随县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

1. 要使式子 $\sqrt{2 - x}$ 有意义，则的取值范围是（）

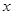A、 $x > 0$ B、 $x \geq - 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 若正比例函数的图象经过点 $(- 1 ， 2)$ ，则这个图象必经过点（）

A、 $(1 ， 2)$ B、 $(- 1 ， - 2)$ C、 $(2 ， - 1)$ D、 $(1 ， - 2)$

查看试题解析

3. 小明同学将某班级毕业升学体育测试成绩（满分30分）统计整理，得到下表，则下列说法错误的是（　　）

分数	20	21	22	23	24	25	26	27	28
人数	2	4	3	8	10	9	6	3	1

A、该组数据的众数是24分 B、该组数据的平均数是25分 C、该组数据的中位数是24分 D、该组数据的极差是8分

查看试题解析

4. 下列说法错误的是（）

A、一组对边平行且相等的四边形是平行四边形. B、四条边都相等的四边形是菱形. C、对角线互相垂直的平行四边形是正方形. D、四个角都相等的四边形是矩形

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{8}$ - $\sqrt{2}$ = $\sqrt{2}$ B、 $\sqrt{4 \frac{1}{9}}$ =2 $\frac{1}{3}$ C、 $\sqrt{5}$ - $\sqrt{3}$ = $\sqrt{2}$ D、 $\sqrt{{(2- \sqrt{5})}^{2}}$ =2- $\sqrt{5}$

查看试题解析
6. 如图，2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》（也称《赵爽弦图》），它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么 $（ a + b ）^{2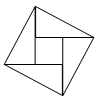}$ 的值为（）

A、13 B、19 C、25 D、169

查看试题解析
7. 函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是（　　）

A、 B、 C、 D、

查看试题解析
8.
如图，正方形ABCD中，AE＝AB，直线DE交BC于点F，则∠BEF＝（）

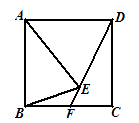A、45° B、30° C、60° D、55°

查看试题解析
9. 如图，在矩形ABCD中，AB=6，BC=8，若将矩形折叠，使B点与D点重合，则折痕EF的长为（）

A、 $\frac{15}{2}$ B、 $\frac{15}{4}$ C、5 D、6

查看试题解析
10. 如图，在 ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S_{四边形DEBC}=2S_△EFB；④∠CFE=3∠DEF，其中正确结论的个数共有（）。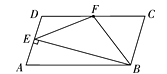

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简： $\sqrt{18 x^{2} y^{3}} (x > 0) =$ .

查看试题解析
12. 已知一个样本：1，3，5，x，2，它的平均数为3，则这个样本的方差是.

查看试题解析
13. 如图，延长正方形 $A B C D$ 的边 $A B$ 到 $E$ ，使 $B E = A C$ ，则 $∠ E =$ 度.

查看试题解析
14. 如图如果以正方形 $A B C D$ 的对角线 $A C$ 为边作第二个正方形 $A C E F$ ，再以对角线 $A E$ 为边作第三个正方形 $A E C H$ ，如此下去，…，已知正方形 $A B C D$ 的面积 $S_{1}$ 为1，按上述方法所作的正方形的面积依次为 $S_{2}$ ， $S_{3}$ … $S_{n}$ （ $n$ 为正整数），那么第8个正方形的面积 $S_{8} =$ .

查看试题解析
15.
如图，将直线y=﹣x沿y轴向下平移后的直线恰好经过点A（2，﹣4），且与y轴交于点B，在x轴上存在一点P使得PA+PB的值最小，则点P的坐标为．

查看试题解析
16. 甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法：①乙先到达青少年宫；②乙的速度是甲速度的2.5倍；③b=480；④a=24.其中正确的是(填序号).

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{3} (\sqrt{2} - \sqrt{3}) - \sqrt{24} - | \sqrt{6} - 3 |$ ；

(2)、已知 $a = 2 - \sqrt{3}$ ，求 $\frac{1 - 2 a + a^{2}}{a - 1} - \frac{\sqrt{a^{2} - 2 a + 1}}{a^{2} - a}$ 的值.

查看试题解析
18. 已知函数 $y = (2 m + 1) x + m - 3$ .

(1)、若这个函数的图象经过原点，求 $m$ 的值

(2)、若这个函数的图象不经过第二象限，求 $m$ 的取值范围.

查看试题解析
19. 阅读下列题目的解题过程：
已知 $a 、 b 、 c$ 为 $Δ A B C$ 的三边，且满足 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，试判断 $Δ A B C$ 的形状.

解：∵ $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$     ①

∴ $c^{2} (a^{2} - b^{2}) = (a^{2} + b^{2}) (a^{2} - b^{2})$         ②

∴ $c^{2} = a^{2} + b^{2}$     ③

∴ $Δ A B C$ 是直角三角形

问：

(1)、上述解题过程，从哪一步开始出现错误？请写出该步的代号：；

(2)、该步正确的写法应是：；

(3)、本题正确的结论为：.

查看试题解析

20. 某中学九年级1班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试. 现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.

项目选择统计图

训练后篮球定时定点投篮测试进球统计表

进球数（个）	8	7	6	5	4	3
人数	2	1	4	7	8	2

请你根据图表中的信息回答下列问题：

(1)、选择长跑训练的人数占全班人数的百分比是，该班共有同学人；

(2)、求训练后篮球定时定点投篮人均进球数；

(3)、根据测试资料，训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%. 请求出参加训练之前的人均进球数.

查看试题解析

21. 如图（1）， $Δ A B C$ 为等腰三角形， $A B = A C = a$ ， $P$ 点是底边 $B C$ 上的一个动点， $P D ∕ ∕ A C$ ， $P E ∕ ∕ A B$ .

(1)、用 $a$ 表示四边形 $A D P E$ 的周长为；

(2)、点 $P$ 运动到什么位置时，四边形 $A D P E$ 是菱形，请说明理由；

(3)、如果 $Δ A B C$ 不是等腰三角形图（2），其他条件不变，点 $P$ 运动到什么位置时，四边形 $A D P E$ 是菱形（不必说明理由）.

查看试题解析
22. 在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）.现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；

（总费用＝广告赞助费+门票费）

方案二：购买门票方式如图所示.

解答下列问题：

(1)、方案一中，y与x的函数关系式为；
方案二中，当0≤x≤100时，y与x的函数关系式为，当x＞100时，y与x的函数关系式为；

(2)、如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；

(3)、甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张.

查看试题解析
23. 数学教科书中，有一个数学活动，其具体操作过程是：
第一步：对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展开（如图1）；

第二步：再一次折叠纸片，使点 $A$ 落在 $E F$ 上，并使折痕经过点 $B$ ，得到折痕 $B M$ ，同时得到线段 $B N$ （如图2）.

请解答以下问题：

(1)、如图2，若延长 $M N$ 交 $B C$ 于 $P$ ， $Δ B M P$ 是什么三角形？请证明你的结论；

(2)、在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP?

(3)、设矩形 $A B C D$ 的边 $A B = 2 ， B C = 4$ ，并建立如图3所示的直角坐标系. 设直线 $B M'$ 为 $y = k x$ ，当 $∠ M' B C = 60 °$ 时，求 $k$ 的值. 此时，将 $Δ A B M'$ 沿 $B M'$ 折叠，点A`是否落在 $E F$ 上（ $E 、 F$ 分别为 $A B$ 、 $C D$ 中点）？为什么？

查看试题解析
24. 如图，直角坐标系xOy中，一次函数y=﹣ $\frac{1}{2}$ x+5的图象l₁分别与x，y轴交于A，B两点，正比例函数的图象l₂与l₁交于点C（m，4）．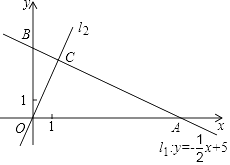

(1)、求m的值及l₂的解析式；

(2)、求S_△_AOC﹣S_△_BOC的值；

(3)、一次函数y=kx+1的图象为l₃ ，且1₁ ， l₂ ， l₃不能围成三角形，直接写出k的值．

查看试题解析