湖北省十堰市竹溪县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-02 类型:期末考试
一、单选题
-
1. 使 有意义的 取值范围是( )A、 B、 C、 D、2. 有一组数据:3,5,5,6,7,这组数据的众数为( )A、5 B、3 C、7 D、63. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列计算正确的是( )A、 B、 C、 D、5. 八(1)班45名同学一天的生活费用统计如下表:
生活费(元)
学生人数(人)
则这45名同学一天的生活费用中,平均数是( )
A、 B、 C、 D、6. 若△ABC中,AB=13,BC=5,AC=12,则下列判断正确的是( )A、∠A=90° B、∠B=90° C、∠C=90° D、△ABC是锐角三角形7. 如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( ) A、6 B、8 C、9 D、108. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形9. 如图,在 中, , ,点 在 上, , ,则 的长为( )
A、6 B、8 C、9 D、108. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形9. 如图,在 中, , ,点 在 上, , ,则 的长为( )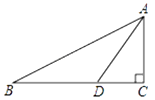 A、 B、 C、 D、10. 一次函数 的图象与 轴、 轴分别交于点 , ,点 , 分别是 , 的中点, 是 上一动点.则 周长的最小值为( )
A、 B、 C、 D、10. 一次函数 的图象与 轴、 轴分别交于点 , ,点 , 分别是 , 的中点, 是 上一动点.则 周长的最小值为( ) A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
11. 计算: .12. 一组数据从小到大排列:0、3、 、5,中位数是4,则 .13. 若点 和点 都在一次函数 的图象上,则 (选择“ ”、“ ”、“ ”填空).14. 在 中, , , ,则斜边 上的高为.15. 在菱形 中,若 , ,则菱形 的周长为.16. 如图,矩形 中, , ,点 是 边上一点,连接 ,把 沿 折叠,使点 落在点 处.当 为直角三角形时,则 的长为.
三、解答题
-
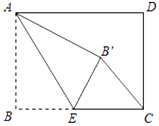
17. 计算:(1)、(2)、18. 直线 过点 ,直线 过点 ,求不等式 的解集.19. 如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.
 20. 某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
20. 某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. (1)、抽样的人数是人,补全频数分布直方图,扇形中 ;(2)、本次调查数据的中位数落在组;(3)、如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?21. 如图,每个小正方形的边长为1,四边形 的每个顶点都在格点上,且 , .
(1)、抽样的人数是人,补全频数分布直方图,扇形中 ;(2)、本次调查数据的中位数落在组;(3)、如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?21. 如图,每个小正方形的边长为1,四边形 的每个顶点都在格点上,且 , .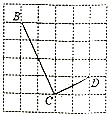 (1)、请在图中补齐四边形 ,并求其面积;(2)、判断 是直角吗?请说明理由22. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)、请在图中补齐四边形 ,并求其面积;(2)、判断 是直角吗?请说明理由22. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G. (1)、求证:DE∥BF;(2)、若∠G=90,求证:四边形DEBF是菱形.23. 电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)、求证:DE∥BF;(2)、若∠G=90,求证:四边形DEBF是菱形.23. 电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: (1)、分别写出当0≤x≤100和x>100时,y与x的函数关系式(2)、利用函数关系式,说明电力公司采取的收费标准(3)、若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?24. 如图,在正方形 中, , 分别是 , 上两个点, .
(1)、分别写出当0≤x≤100和x>100时,y与x的函数关系式(2)、利用函数关系式,说明电力公司采取的收费标准(3)、若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?24. 如图,在正方形 中, , 分别是 , 上两个点, . (1)、如图1, 与 的关系是;(2)、如图2,当点 是 的中点时,(1)中的结论是否仍然成立,若成立,请进行证明;若不成立,说明理由;(3)、如图2,当点 是 的中点时,求证: .25. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , ,且点 的坐标为 ,点 为 的中点.
(1)、如图1, 与 的关系是;(2)、如图2,当点 是 的中点时,(1)中的结论是否仍然成立,若成立,请进行证明;若不成立,说明理由;(3)、如图2,当点 是 的中点时,求证: .25. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , ,且点 的坐标为 ,点 为 的中点. (1)、点 的坐标是 , 点 的坐标是;(2)、直线 上有一点 ,若 ,试求出点 的坐标;(3)、若点 为直线 上的一个动点,过点 作 轴的垂线,与直线 交于点 ,设点 的横坐标为 ,线段 的长度为 ,求 与 的函数解析式.
(1)、点 的坐标是 , 点 的坐标是;(2)、直线 上有一点 ,若 ,试求出点 的坐标;(3)、若点 为直线 上的一个动点,过点 作 轴的垂线,与直线 交于点 ,设点 的横坐标为 ,线段 的长度为 ,求 与 的函数解析式.