湖北省荆州市松滋市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-02 类型:期末考试
一、单选题
-
1. 若二次根式 在实数范围内有意义,则a的取值范围是( )A、a>1 B、a≥1 C、a=1 D、a≤12. 下列二次根式中能与2 合并的是( )A、 B、 C、 D、3. 若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )A、4 B、3 C、5 D、64. 下列选项中,不能判定四边形ABCD是平行四边形的是
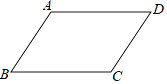 A、 , B、 , C、 , D、 ,5. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采取全面调查的方式 B、一组数据1、2、5、5、5、3、3的中位数和众数都是5 C、投掷一枚硬币100次,一定有50次“正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定6. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AD,AC的中点,若CB=4,则EF的长度为( )
A、 , B、 , C、 , D、 ,5. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采取全面调查的方式 B、一组数据1、2、5、5、5、3、3的中位数和众数都是5 C、投掷一枚硬币100次,一定有50次“正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定6. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AD,AC的中点,若CB=4,则EF的长度为( )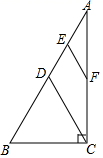 A、2 B、1 C、 D、27. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、
A、2 B、1 C、 D、27. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、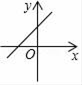 B、
B、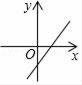 C、
C、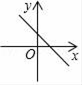 D、
D、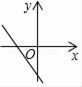 8. 如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
8. 如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( ) A、14 B、13 C、14 D、149. 如图,在矩形ABCD中,E为AD的中点,∠BED的平分线交BC于点F,若AB=3,BC=8,则FC的长度为( )
A、14 B、13 C、14 D、149. 如图,在矩形ABCD中,E为AD的中点,∠BED的平分线交BC于点F,若AB=3,BC=8,则FC的长度为( )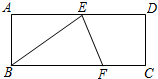 A、6 B、5 C、4 D、310. 在平面直角坐标系内,已知点A的坐标为(-6,0),直线l:y=kx+b不经过第四象限,且与x轴的夹角为30°,点P为直线l上的一个动点,若点P到点A的最短距离是2,则b的值为( )A、 或 B、 C、2 D、2 或10
A、6 B、5 C、4 D、310. 在平面直角坐标系内,已知点A的坐标为(-6,0),直线l:y=kx+b不经过第四象限,且与x轴的夹角为30°,点P为直线l上的一个动点,若点P到点A的最短距离是2,则b的值为( )A、 或 B、 C、2 D、2 或10二、填空题
-
11. 计算:(− )2=; =.12. 若点A(2,m)在平面直角坐标系的x轴上,则点P(m-1,m+3)到原点O的距离为.13. 小华用S2= {(x1-8)2+(x2-8)2+……+(x10-8)2计算一组数据的方差,那么x1+x2+x3+…+x10=.14. 一个有进水管与出水管的容器,从某时刻开始,2min内只进水不出水,在随后的4min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则每分钟出水升.
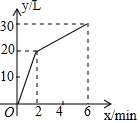 15. 如图,在矩形ABCD中,按以下步骤作图:①分别以点A和点C为圆心,以大于 AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=.
15. 如图,在矩形ABCD中,按以下步骤作图:①分别以点A和点C为圆心,以大于 AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=.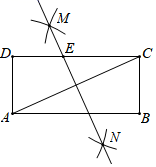 16. 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=10cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为cm.
16. 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=10cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为cm.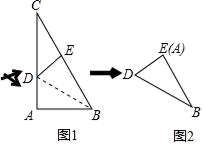
三、解答题
-
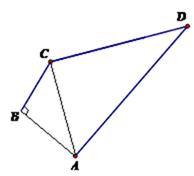
17. 计算题(1)、(2)、18. 已知 ,求 的值.19. 如图,在四边形ABCD中, AB=4,BC=3,CD=12,AD=13,∠B=90°,连接AC.求四边形ABCD的面积.
 20. 某中学九年级开展“社会主义核心价值观”演讲比赛活动,九(1)班、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出5名选手的复赛成绩(满分100分)如图所示.
20. 某中学九年级开展“社会主义核心价值观”演讲比赛活动,九(1)班、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出5名选手的复赛成绩(满分100分)如图所示.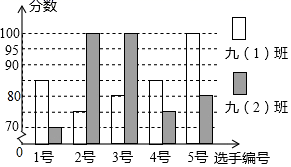
根据图中数据解决下列问题:
(1)、九(1)班复赛成绩的众数是分,九(2)班复赛成绩的中位数是分;(2)、请你求出九(1)班和九(2)班复赛的平均成绩和方差,并说明哪个班的成绩更稳定.21. 在数学学习中,及时对知识进行归纳和整理是提高学习效率的重要方法,善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,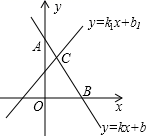
把相关知识归纳整理如下:
一次函数与方程(组)的关系:
①一次函数的解析式就是一个二元一次方程;
②点B的横坐标是方程kx+b=0的解;
③点C的坐标(x,y)中x,y的值是方程组①的解.
一次函数与不等式的关系:
①函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式kx+b>0的解集;
②函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式②的解集.
(1)、请你根据以上归纳整理的内容在下面的数字序号后写出相应的结论:①;②;(2)、如果点B坐标为(2,0),C坐标为(1,3);①直接写出kx+b≥k1x+b1的解集;
②求直线BC的函数解析式.
22. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.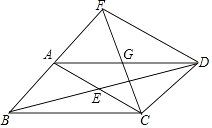 (1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
(1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
23. A城有肥料400t,B城有肥料600t,现要把这些肥料全部运往C、D两乡,所需运费如下表所示:城市
A城
B城
运往C乡运费(元/t)
20
15
运往D乡运费(元/t)
25
24
现C乡需要肥料480t,D乡需要肥料520t.
(1)、设从A城运往C乡肥料x吨,总运费为y元;①求B城运往C、D两乡的肥料分别为多少吨?(用含x的式子表示).
②写出y关于x的函数解析式,并求出最少总运费.
(2)、由于更换车型,使A城运往C乡的运费每吨减少m元(0<m<6),这时怎样调运才能使总运费最少?24. 如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.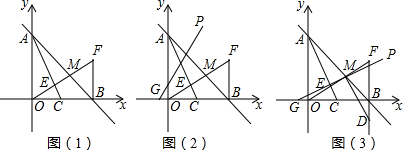 (1)、直接写出点F的坐标(用m表示);(2)、求证:OF⊥AC;(3)、如图(2),若m=2,点G的坐标为(- ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
(1)、直接写出点F的坐标(用m表示);(2)、求证:OF⊥AC;(3)、如图(2),若m=2,点G的坐标为(- ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;①求k的取值范围;
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.