湖北省恩施市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-02 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 若一个三角形的三边长为 ,则使得此三角形是直角三角形的的值是( )A、 B、 C、 D、 或3. 某班数学兴趣小组8名同学的毕业升学体育测试成绩依次为:30,29,28,27,28,29,30,28,这组数据的众数是( )A、27 B、28 C、29 D、304. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 5. 正方形具有而菱形不一定具有的性质是( )A、四边相等 B、对角线相等 C、对角线互相垂直 D、对角线互相平分6. 直线y=-3x+2经过的象限为( )A、第一、二、四象限 B、第一、二、三象限 C、第一、三、四象限 D、第二、三、四象限7. 如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A,C两点之间的距离为( )
5. 正方形具有而菱形不一定具有的性质是( )A、四边相等 B、对角线相等 C、对角线互相垂直 D、对角线互相平分6. 直线y=-3x+2经过的象限为( )A、第一、二、四象限 B、第一、二、三象限 C、第一、三、四象限 D、第二、三、四象限7. 如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A,C两点之间的距离为( ) A、4米 B、 米 C、8米 D、 米8. 若式子 有意义,则一次函数 的图象可能是( )A、
A、4米 B、 米 C、8米 D、 米8. 若式子 有意义,则一次函数 的图象可能是( )A、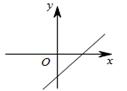 B、
B、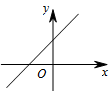 C、
C、 D、
D、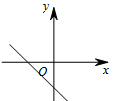 9. 已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )A、( , ) B、( , ) C、(-3,-1) D、(-3, )10. A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时刻t(小时)之间的关系.下列说法:
9. 已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )A、( , ) B、( , ) C、(-3,-1) D、(-3, )10. A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时刻t(小时)之间的关系.下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时;
④乙先到达B地.
其中正确的个数是( )
A、1 B、2 C、3 D、411. 如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC边上的中点,连接EF.若 ,BD=4,则菱形ABCD的周长为( ) A、4 B、 C、 D、2812. 如图,点A,B,C在一次函数 的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A、4 B、 C、 D、2812. 如图,点A,B,C在一次函数 的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( ) A、1 B、3 C、 D、
A、1 B、3 C、 D、二、填空题
-
13. 计算: 的结果是.14. 一次函数 与 的图象如图,则 的解集是.
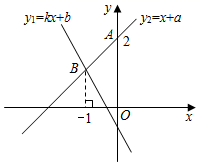 15. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm.
15. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm.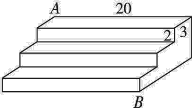 16. 如图放置的两个正方形的边长分别为4和8,点G为CF中点,则AG的长为.
16. 如图放置的两个正方形的边长分别为4和8,点G为CF中点,则AG的长为.
三、解答题
-
17.(1)、计算:(2)、先化简,再求值:已知 ,试求 的值.18. 已知长方形的长 ,宽 .(1)、求长方形的周长;(2)、求与长方形等面积的正方形的周长,并比较其与长方形周长的大小关系.19. 为了让同学们了解自己的体育水平,八年级1班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
八年级1班全体女生体育测试成绩分布扇形统计图

八年级全体男生体育测试成绩条形统计图

八年级 班体育模拟测试成绩分析表

根据以上信息,解答下列问题:
(1)、这个班共有男生人,共有女生人;(2)、补全八年级 班体育模拟测试成绩分析表;(3)、你认为在这次体育测试中,1班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.20. 在平行四边形ABCD中,AC的垂直平分线分别交AD,BC于F,E两点,交AC于O点,试判断四边形AECF的形状,并说明理由. 21. 武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
21. 武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示 (1)、求甲、乙两种收费方式的函数关系式;(2)、当印刷多少份学案时,两种印刷方式收费一样?22. 如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD(1)、求AD的长;(2)、若∠C=30°,求CD的长.
(1)、求甲、乙两种收费方式的函数关系式;(2)、当印刷多少份学案时,两种印刷方式收费一样?22. 如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD(1)、求AD的长;(2)、若∠C=30°,求CD的长. 23. 某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.
23. 某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.A
B
成本(元)
50
35
售价(元)
70
50
(1)、请写出y关于x的函数关系式;(2)、如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?24. 已知:如图1,在平面直角坐标系中,直线 与坐标轴分别相交于点A、B,与直线 相交于点C.
 (1)、求点C的坐标;(2)、若平行于y轴的直线 交于直线l1于点E,交直线l2于点D,交 轴于点M,且 ,求a的值;(3)、如图2,点P是第四象限内一点,且 ,连接AP,探究AP与BP之间的位置关系,并证明你的结论.
(1)、求点C的坐标;(2)、若平行于y轴的直线 交于直线l1于点E,交直线l2于点D,交 轴于点M,且 ,求a的值;(3)、如图2,点P是第四象限内一点,且 ,连接AP,探究AP与BP之间的位置关系,并证明你的结论.