河南省濮阳市县区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

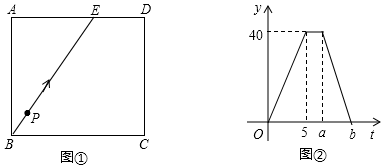
1. 生物学家发现：生物具有遗传多样性，遗传密码大多储存在 $D N A$ 分子上.一个 $D N A$ 分子的直径约为0.0000002 $cm$ ，这个数用科学记数法可以表示为（）

A、 $0.2 \times 10^{- 6}$ B、 $2 \times 10^{- 7}$ C、 $0.2 \times 10^{- 7}$ D、 $2 \times 10^{-8}$

查看试题解析
2. 下列因式分解错误的是（）

A、2x（x﹣2）+（2﹣x）=（x﹣2）（2x+1） B、x²+2x+1=（x+1）² C、x²y﹣xy²=xy（x﹣y） D、x²﹣y²=（x+y）（x﹣y）

查看试题解析
3. 下列数据中不能作为直角三角形的三边长是（）

A、1、1、 $\sqrt{2}$ B、5、12、13 C、3、5、7 D、6、8、10

查看试题解析
4. 若式子 $\frac{| x | - 2}{x^{2} + 4 x + 4}$ 的值等于0，则x的值为（）

A、±2 B、－2 C、2 D、－4

查看试题解析
5. 若a，b为等腰△ABC的两边，且满足|a﹣5|+ $\sqrt{b - 2}$ ＝0，则△ABC的周长为（　　）

A、9 B、12 C、15或12 D、9或12

查看试题解析
6. 对于两组数据A，B，如果s_A²＞s_B² ，且 $\bar{x_{A}} = \bar{x_{B}}$ ，则（）

A、这两组数据的波动相同 B、数据B的波动小一些 C、它们的平均水平不相同 D、数据A的波动小一些

查看试题解析
7. 函数 $y = \frac{x}{\sqrt{x + 3}}$ 的自变量取值范围是（）

A、x≠0 B、x＞﹣3 C、x≥﹣3且x≠0 D、x＞﹣3且x≠0

查看试题解析
8. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

查看试题解析
9. 如果ab＞0，a＋b＜0，那么下面各式：① $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ ； ② $\sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{a}}$ ＝1；③ $\sqrt{a b} \div \sqrt{\frac{a}{b}}$ ＝－b.其中正确的是（）

A、①② B、①③ C、①②③ D、②③

查看试题解析
10. 已知：如图①，长方形ABCD中，E是边AD上一点，且AE=6cm，点P从B出发，沿折线BE-ED-DC匀速运动，运动到点C停止．P的运动速度为2cm/s，运动时间为t（s），△BPC的面积为y（cm²），y与t的函数关系图象如图②，则下列结论正确的有（）
①a=7②AB=8cm③b=10④当t=10s时，y=12cm²

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 如果一个多边形的每一个外角都等于 $30^{\circ}$ ，则它的内角和是 $^{\circ}$ .

查看试题解析
12. 已知一次函数y=（-1-a²）x+1的图象过点（x₁ ， 2），（x₂ ， -1），则x₁与x₂的大小关系为 .

查看试题解析
13. 计算： ${(- \sqrt{3})}^{2} + | - 4 | \times 2^{- 1} - {(\sqrt{2} - 1)}^{0} =$ .

查看试题解析
14. 已知一组数据6，6，5，x，1，请你给正整数x一个值，使这组数据的众数为6，中位数为5.

查看试题解析
15. 菱形 $A B C D$ 中， $∠ B = 60^{\circ}$ ， $A B = 5$ ，以 $A C$ 为边长作正方形 $A C F E$ ，则点 $D$ 到 $E F$ 的距离为.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{x^{2} - 2 x + 1}{x^{2} - x} + \frac{x^{2} - 4}{x^{2} + 2 x}) \div \frac{2}{x}$ ，且 $x$ 为满足 $- 2 \leq x < 2$ 的整数.

查看试题解析

17.

2019

年

4

月

23

日是第

24

个世界读书日，为迎接第

24

个世界读书日的到来，某校举办读书分享大赛活动：大赛以“推荐分享”为主题，参赛者选择一本自己最喜欢的书，然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分（各项成绩均按百分制），综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示；

参赛者	推荐语	读书心得	读书讲座
甲	$85$	$83$	$93$
乙	$92$	$86$	$86$

(1)、若将三项成绩的平均分作为参赛选手的综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由.

(2)、若“推荐语”“读书心得”“读书讲座”的成绩按

2 : 3 : 5

确定综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由.

查看试题解析

18. 已知：如图，正方形 $A B C D$ 中， $P$ 是边 $B C$ 上一点， $B E ⊥ A P$ ， $D F ⊥ A P$ ，垂足分别是点 $E$ 、 $F$ .

(1)、求证： $E F = A E - B E$ ；

(2)、连接 $B F$ ，若 $A D = 5$ ， $A F = 3$ ，求 $B F$ 的长.

查看试题解析
19. 如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

(1)、求证：四边形AMDN是平行四边形；

(2)、填空：①当AM的值为时，四边形AMDN是矩形；②当AM的值为时，四边形AMDN是菱形.

查看试题解析
20. 端午节放假期间，某学校计划租用 $6$ 辆客车送 $240$ 名师生参加研学活动，现有甲、乙两种客车，它们的载客量和租金如下表，设租用甲种客车 $x$ 辆，租车总费用为 $y$ 元.

甲种客车

乙种客车

载客量（人/辆）

$45$

$30$

租金（元/辆）

$280$

$200$

(1)、求出 $y$ （元）与 $x$ （辆）之间函数关系式；

(2)、求出自变量的取值范围；

(3)、选择怎样的租车方案所需的费用最低？最低费用多少元？

查看试题解析
21. 如图，矩形 $A B C D$ 中， $A B = 8$ ， $B C = 6$ ， $P$ 为 $A D$ 上一点，将 $Δ A B P$ 沿 $B P$ 翻折至 $Δ E B P$ ， $P E$ 与 $C D$ 相交于点 $O$ ， $B E$ 与 $D C$ 相交于 $G$ 点，且 $O E = O D$ .

(1)、求证： $A P = D G$ ；

(2)、求 $A P$ 的长度.

查看试题解析
22. 实验中学学生在学习等腰三角形性质“三线合一”时

(1)、（探究发现）如图1，在△ABC中，若AD平分∠BAC，AD⊥BC时，可以得出AB＝AC，D为BC中点，请用所学知识证明此结论.

(2)、（学以致用）如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B，如图2，若顶点C与顶点F也重合，且∠BFE＝ $\frac{1}{2}$ ∠ACB，试探究线段BE和FD的数量关系，并证明.

(3)、（拓展应用）如图3，若顶点C与顶点F不重合，但是∠BFE＝ $\frac{1}{2}$ ∠ACB仍然成立，（学以致用）中的结论还成立吗？证明你的结论.

查看试题解析
23. 如图，直线 $l_{1}$ 的函数解析式为 $y = - 2 x + 4$ ，且 $l_{1}$ 与 $x$ 轴交于点 $D$ ，直线 $l_{2}$ 经过点 $A$ 、 $B$ ，直线 $l_{1}$ 、 $l_{2}$ 交于点 $C$ .

(1)、求直线 $l_{2}$ 的函数解析式；

(2)、求 $Δ A D C$ 的面积；

(3)、在直线 $l_{2}$ 上是否存在点 $P$ ，使得 $Δ A D P$ 面积是 $Δ A D C$ 面积的 $1.5$ 倍？如果存在，请求出 $P$ 坐标；如果不存在，请说明理由.

查看试题解析

	甲种客车	乙种客车
载客量（人/辆）	$45$	$30$
租金（元/辆）	$280$	$200$