河南省平顶山市叶县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-02 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 若一个多边形的内角和等于外角和的2倍,则这个多边形的边数为( )A、8 B、6 C、5 D、44. 若式子 有意义,则实数 的取值范围是( )A、 且 B、 C、 D、5. 在平面直角坐标系中,点 )平移后能与原来的位置关于 轴对称,则应把点 ( )A、向右平移 个单位 B、向左平移 个单位 C、向右平移 个单位 D、向左平移 个单位6. 如图,已知直线 与 的交点的横坐标为
2. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 若一个多边形的内角和等于外角和的2倍,则这个多边形的边数为( )A、8 B、6 C、5 D、44. 若式子 有意义,则实数 的取值范围是( )A、 且 B、 C、 D、5. 在平面直角坐标系中,点 )平移后能与原来的位置关于 轴对称,则应把点 ( )A、向右平移 个单位 B、向左平移 个单位 C、向右平移 个单位 D、向左平移 个单位6. 如图,已知直线 与 的交点的横坐标为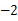 ,根据图象有下列3个结论:① ;② ;③ 是不等式 的解集
,根据图象有下列3个结论:① ;② ;③ 是不等式 的解集  其中正确的个数是( )
其中正确的个数是( )  A、0, B、1, C、2, D、37. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在 中, 、 是 的中线, 与 相交于点 ,点 、 分别是 、 的中点,连接 .若, , 则四边形 的周长是( )
A、0, B、1, C、2, D、37. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在 中, 、 是 的中线, 与 相交于点 ,点 、 分别是 、 的中点,连接 .若, , 则四边形 的周长是( ) A、 B、 C、 D、9. 某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )A、每天比原计划多铺设10米,结果延期20天完成 B、每天比原计划少铺设10米,结果延期20天完成 C、每天比原计划多铺设10米,结果提前20天完成 D、每天比原计划少铺设10米,结果提前20天完成10. 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
A、 B、 C、 D、9. 某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )A、每天比原计划多铺设10米,结果延期20天完成 B、每天比原计划少铺设10米,结果延期20天完成 C、每天比原计划多铺设10米,结果提前20天完成 D、每天比原计划少铺设10米,结果提前20天完成10. 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( ) A、105° B、112.5° C、120° D、135°
A、105° B、112.5° C、120° D、135°二、填空题
-
11. 分解因式: .12. 当x=时,分式 的值等于零.13. 关于x的方程 =3有增根,则m的值为.14. 如图,已知 的顶点 , ,点 在 轴正半轴上,按以下步骤作图:①以点 为圆心,适当长度为半径作弧,分别交边 , 于点 , ;②分别以点 , 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ;③作射线 ,交边 于点 ,则点 的坐为.
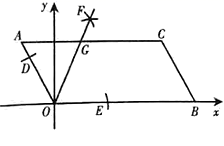 15. 如图,在 中, , , 的面积是16, 边的垂直平分线 分别交 , 边于点E,F.若点D为 边的中点,点M为线段 上一动点,则 周长的最小值为.
15. 如图,在 中, , , 的面积是16, 边的垂直平分线 分别交 , 边于点E,F.若点D为 边的中点,点M为线段 上一动点,则 周长的最小值为.
三、解答题
-
16. 解方程与不等式组(1)、解方程:(2)、解不等式组17. 先化简 ,然后从 , , , 中选择一个合适的数作为 的值代入求值18. 如图, 是等边三角形, 是中线,延长 至 , .
 (1)、求证: ;(2)、请在图中过点 作 交 于 ,若 ,求 的周长.19. 某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的 倍,所购数量比第一批多100套.(1)、求第一批套尺购进时单价是多少?(2)、若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?20. 如图,已知 的三个顶点坐标为 , , .
(1)、求证: ;(2)、请在图中过点 作 交 于 ,若 ,求 的周长.19. 某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的 倍,所购数量比第一批多100套.(1)、求第一批套尺购进时单价是多少?(2)、若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?20. 如图,已知 的三个顶点坐标为 , , . (1)、将 绕坐标原点 旋转 ,画出旋转后的 ,并写出点 的对应点 的坐标;(2)、将 绕坐标原点 逆时针旋转 ,直接写出点 的对应点Q的坐标;(3)、请直接写出:以 、 、 为顶点的平行四边形的第四个顶点 的坐标.21. 如图,将 沿过点 的直线 折叠,使点 落到 边上的 处,折痕交 边于点 ,连接 .
(1)、将 绕坐标原点 旋转 ,画出旋转后的 ,并写出点 的对应点 的坐标;(2)、将 绕坐标原点 逆时针旋转 ,直接写出点 的对应点Q的坐标;(3)、请直接写出:以 、 、 为顶点的平行四边形的第四个顶点 的坐标.21. 如图,将 沿过点 的直线 折叠,使点 落到 边上的 处,折痕交 边于点 ,连接 . (1)、求证:四边形 是平行四边形;(2)、若 平分 ,求证: .22. 某水果店经销进价分别为 元/千克、 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
(1)、求证:四边形 是平行四边形;(2)、若 平分 ,求证: .22. 某水果店经销进价分别为 元/千克、 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)时间
甲水果销量
乙水果销量
销售收入
周五
千克
千克
元
周六
千克
千克
元
(1)、求甲、乙两种水果的销售单价;(2)、若水果店准备用不多于 元的资金再购进两种水果共 千克,求最多能够进甲水果多少千克?(3)、在(2)的条件下,水果店销售完这 千克水果能否实现利润为 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.23. 如图,在 中, ,D在边AC上,且 .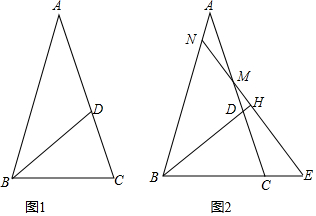 (1)、如图1,填空 ,(2)、如图2,若M为线段AC上的点,过M作直线 于H,分别交直线AB、BC与点N、E.
(1)、如图1,填空 ,(2)、如图2,若M为线段AC上的点,过M作直线 于H,分别交直线AB、BC与点N、E.求证: 是等腰三角形;
试写出线段AN、CE、CD之间的数量关系,并加以证明.