河南省南阳市唐河县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值等于

A、0 B、3 C、-3 D、3

查看试题解析
2. “厉害了，华为!”2019 年 1 月 7 日，华为宣布推出业界最高性能 ABM- based 处理器—鲲鹏 920.据了解，该处理器采用 7 纳米制造工艺，已知 1 纳米=0.000 000 001 米，则 7 纳米用科学记数法表示为（）

A、7×10^-9 米 B、7×10 ^-8 米 C、7×10 ⁸ 米 D、0.7×10^-8 米

查看试题解析
3. 下列说法正确的是(　　)

A、形如 $\frac{A}{B}$ 的式子叫分式 B、整式和分式统称有理式 C、当x≠3时，分式 $\frac{x}{x - 3}$ 无意义 D、分式 $\frac{2}{a^{2} b}$ 与 $\frac{1}{a b}$ 的最简公分母是a³b²

查看试题解析
4. 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据，如下表：

甲

2

6

7

7

8

乙

2

3

4

8

8

关于以上数据，说法正确的是（　　）

A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数小于乙的平均数 D、甲的方差小于乙的方差

查看试题解析
5. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（）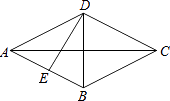

A、2.4cm B、4.8cm C、5cm D、9.6cm

查看试题解析
6. 直线l₁：y=kx+b与直线l₂：y=bx+k在同一坐标系中的大致位置是（　　）

A、 B、 C、 D、

查看试题解析
7. “绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（）

A、 $\frac{60}{x} - \frac{60}{(1 + 25 %) x} = 30$ B、 $\frac{60}{(1 + 25 %) x} - \frac{60}{x} = 30$ C、 $\frac{60 \times (1 + 25 %)}{x} - \frac{60}{x} = 30$ D、 $\frac{60}{x} - \frac{60 \times (1 + 25 %)}{x} = 30$

查看试题解析
8. 如图，在正方形 $A B C D$ 中， $E$ 是 $A C$ 上的一点，且 $A B = A E$ ，则 $∠ E B C$ 的度数是（）

A、20度 B、22.5度 C、30度 D、45度

查看试题解析
9. 如图是我市某一天内的气温变化图，根据图象，下列说法中错误的是(　　)

A、这一天中最高气温是26℃ B、这一天中最高气温与最低气温的差为16℃ C、这一天中2时至14时之间的气温在逐渐升高 D、这一天中14时至24时之间的气温在逐渐降低

查看试题解析
10. 如图，点 $E$ 为菱形 $A B C D$ 边上的一个动点，并沿 $A$ → $B$ → $C$ → $D$ 的路径移动，设点E经过的路径长为 $x$ ， $△ A D E$ 的面积为 $y$ ，则下列图象能大致反映 $y$ 与 $x$ 的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 计算： ${(- 1)}^{2019} + {(4 - π)}^{0} - {(\frac{1}{2})}^{- 2} =$ .

查看试题解析
12. “暑期乒乓球夏令营”开始在学校报名了，已知甲、乙、丙三个夏令营组人数相等，且每组学生的平均年龄都是14岁，三个组学生年龄的方差分别是 $S_{甲}^{2} = 17$ ， $S_{乙}^{2} = 14.6$ ， $S_{丙}^{2} = 19$ 如果今年暑假你也准备报名参加夏令营活动，但喜欢和年龄相近的同伴相处，那么你应选择是.

查看试题解析
13.
如图，在矩形ABCD中，BC=20cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和2cm/s，则最快 s后，四边形ABPQ成为矩形．

查看试题解析
14. 如图，点A，B在反比例函数y＝ $\frac{1}{x}$ (x＞0)的图象上，点C，D在反比例函数y＝ $\frac{k}{x}$ (k＞0)的图象上，AC∥BD∥y轴，已知点A，B的横坐标分别为1，2，△OAC与△ABD的面积之和为 $\frac{3}{2}$ ，则k的值为.

查看试题解析
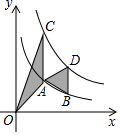15. 如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为．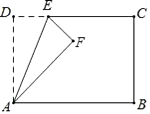

查看试题解析

三、解答题

16. 先化简 $(\frac{a}{a - 1} - 1) \div \frac{2}{a^{2} - a}$ ，然后从 $- 2 \leq a < 2$ 中选出一个合适的整数作为 $a$ 的值代入求值.

查看试题解析

17. 某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.

收集数据

从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：

甲 78 86 74 81 75 76 87 70 75 90

75 79 81 70 74 80 86 69 83 77

乙 93 73 88 81 72 81 94 83 77 83

80 81 70 81 73 78 82 80 70 40

(1)、整理、描述数据

按如下分数段整理、描述这两组样本数据：

成绩 $x$

人数

部门

40≤x≤49

50≤x≤59

60≤x≤69

70≤x≤79

80≤x≤89

90≤x≤100

甲

乙

（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）

(2)、分析数据

两组样本数据的平均数、中位数、众数如下表所示：

部门	平均数	中位数	众数
甲	78.3	77.5	75
乙	78	80.5	81

得出结论：

$a$ .估计乙部门生产技能优秀的员工人数为；

$b$ .可以推断出部门员工的生产技能水平较高，理由为.（至少从两个不同的角度说明推断的合理性）

查看试题解析

18. 如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE．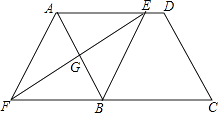

(1)、求证：△AGE≌△BGF；

(2)、试判断四边形AFBE的形状，并说明理由．

查看试题解析
19. 某八年级计划用360元购买笔记本奖励优秀学生，在购买时发现，每本笔记本可以打九折，结果买得的笔记本比打折前多10本。

(1)、请求出每本笔记本的原来标价；

(2)、恰逢文具店周年志庆，每本笔记本可以按原价打8折，这样该校最多可购入多少本笔记本？

查看试题解析
20. 如图，在平面直角坐标系中，O为坐标原点，▱AOBC的顶点A、C的坐标分别为A（﹣2，0）、C（0，3），反比例函数的图象经过点B.

(1)、求反比例函数的表达式；

(2)、这个反比例函数的图象与一个一次函数的图象交于点B、D（m，1），根据图象回答：当x取何值时，反比例函数的值大于一次函数的值.

查看试题解析
21. 已知 $A 、 B$ 两地相距 $60 k m$ ，甲、乙两人沿同一公路从 $A$ 地出发到 $B$ 地，甲骑摩托车，乙骑自行车，如图中 $C D ， O E$ 分别表示甲、乙离开 $A$ 地的距离 $y (k m)$ 与时间 $| x (h) |$ 的函数关系的图象，结合图象解答下列问题.

(1)、甲比乙晚出发小时，乙的速度是 $km / h$ ；甲的速度是 $km / h$ .

(2)、若甲到达 $B$ 地后，原地休息0.5小时，从 $B$ 地以原来的速度和路线返回 $A$ 地，求甲、乙两人第二次相遇时距离 $A$ 地多少千米？并画出函数关系的图象.

查看试题解析
22. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．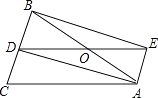

(1)、求证：四边形AEBD是矩形；

(2)、当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由

查看试题解析
23. 如图，在平面直角坐标系中， $O$ 为坐标原点，矩形 $O A B C$ 的顶点 $A (12 ， 0)$ 、 $C (0 ， 9)$ ，将矩形 $O A B C$ 的一个角沿直线 $B D$ 折叠，使得点 $A$ 落在对角线 $O B$ 上的点 $E$ 处，折痕与 $x$ 轴交于点 $D$ .

(1)、求线段 $O B$ 的长度；

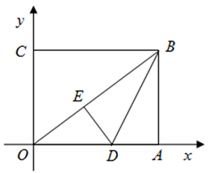(2)、求直线 $B D$ 所对应的函数表达式；

(3)、若点 $Q$ 在线段 $B D$ 上，在线段 $B C$ 上是否存在点 $P$ ，使以 $D 、 E 、 P 、 Q$ 为顶点的四边形是平行四边形？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析