河南省南阳市内乡县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各点中，位于第四象限的点是（）

A、(3,-4) B、(3,4) C、(-3,4) D、(-3,-4)

查看试题解析
2. 下列代数式变形正确的是（　　）

A、 $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x - y}$ B、 $\frac{- x + y}{2} = - \frac{x + y}{2}$ C、 $\frac{1}{x y} \div (\frac{1}{x} + \frac{1}{y}) = \frac{1}{y} + \frac{1}{x}$ D、 $\frac{x - y}{x + y} = \frac{x^{2} - y^{2}}{{(x + y)}^{2}}$

查看试题解析
3. 如图，下面不能判定四边形ABCD是平行四边形的是（）

A、 $AB / / CD ， AB = CD$ B、 $A B = C D ， A D = B C$ C、 $∠ B + ∠ DAB = 180^{°} ， AB = CD$ D、 $∠ B = ∠ D ， ∠ BCA = ∠ DAC$

查看试题解析
4. 小明调查了班级里20位同学本学期购买课外书的花费情况，并将结果绘制成了如图的统计图.在这20位同学中，本学期购买课外书的花费的众数和中位数分别是（　　）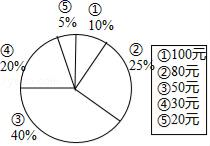

A、50，50 B、50，30 C、80，50 D、30，50

查看试题解析
5. 已知菱形的面积为10，对角线的长分别为x和y，则y关于x的函数图象是 $($ $)$

A、 B、 C、 D、

查看试题解析
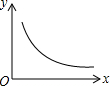6. 如图，在矩形ABCD中，点E是AD中点，且 $AE = 2$ ，BE的垂直平分线MN恰好过点C，则矩形的一边AB的长度为（）

A、2 B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、4

查看试题解析
7. 已知方程 $\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$ 无解，则m的值为（）

A、0 B、3 C、6 D、2

查看试题解析
8. 如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E.若∠CBF＝20°，则∠DEF的度数是（）

A、25° B、40° C、45° D、50°

查看试题解析
9. 如图，双曲线 $y = \frac{m}{x}$ 与直线 $y = k x + b$ 交于点M，N，并且点M坐标为(1，3)点N坐标为(-3，-1)，根据图象信息可得关于x的不等式 $\frac{m}{x} < kx + b$ 的解为（）

A、 $x < - 3$ B、 $- 3 < x < 0$ C、 $x < - 3 或 0 < x < 1$ D、 $- 3 < x < 0 或 x > 1$

查看试题解析
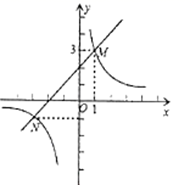10. 如图，矩形ABCD中， E是AD的中点，将 $Δ ABE$ 沿直线BE折叠后得到 $Δ GBE$ ，延长BG交CD于点F若 $AB = 6 ， BC = 10$ ，则FD的长为（）

A、3 B、 $\frac{7}{2}$ C、 $\frac{25}{6}$ D、 $\frac{25}{4}$

查看试题解析

二、填空题

11. 要使分式 $\frac{2}{1 - x}$ 的值为1，则x应满足的条件是

查看试题解析
12. 计算：（π﹣3.14）⁰+3^﹣¹＝.

查看试题解析
13. 反比例函数y= $\frac{k}{x}$ (k＞0)在第一象限内的图象如图，点M是图象上一点，MP垂直x轴于点P，如果△MOP的面积为1，那么k的值是.

查看试题解析
14. 如图，在菱形ABCD中，∠BAD=120°，CF⊥AD于点E，且BC=CF，连接BF交对角线AC于点M，则∠FMC= ．

查看试题解析
15. 如图，正方形ABCD中， $AB = 4 cm$ ，点E、F分别在边AD和边BC上，且 $BF = ED = 3 cm$ ，动点P、Q分别从A、C两点同时出发，点P自A→F→B方向运动，点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s，3cm/s，设运动时间为 $t (0 < t ⩽ 8)$ ，当A 、C、P、Q四点为顶点的四边形是平行四边形时则t=

查看试题解析

三、解答题

16. 先化简，再求值:( $(\frac{3}{a + 2} + a - 2) \div \frac{a^{2} + 2 a + 1}{a + 2}$ ，其中 $a = 3$ 。

查看试题解析
17. 某学校八年级开展英语拼写大赛，一班和二班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示：

(1)、根据图示填写下表

班级

中位数（分）

众数（分）

平均数（分）

一班

85

二班

100

85

(2)、结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩比较好？

(3)、已知一班的复赛成绩的方差是70，请求出二班复试成绩的方差，并说明哪个班成绩比较稳定？

查看试题解析
18. 在平行四边形 $A B C D$ 中， $AE ⊥ BC$ 于E， $AF ⊥ CD$ 于F.若 $AE = 4 ， AF = 6$ ，平行四边形 $A B C D$ 周长为40，求平行四边形 $A B C D$ 的面积.

查看试题解析
19. 服装店去年10月以每套500元的进价购进一批羽绒服，当月以标价销售，销售额14000元进入11月份搞促销活动，每件降价50元，这样销售额比10月份增加了5500元，售出的件数是10月份的1.5 倍，求每件羽绒服的标价是多少元.

查看试题解析
20. 如图，在 $Rt Δ ABC$ 中， $∠ ACB = 90^{°}$ ，E为CA延长线上一点，D为AB上一点，F为 $Δ ABC$ 外一点且 $AC = AE = AF = AD = 1 ， EF / / AB$ 连接DF，BF.

(1)、当 $∠ CAB$ 的度数是多少时，四边形ADFE为菱形，请说明理由：

(2)、当AB=时，四边形ACBF为正方形(请直接写出)

查看试题解析
21. 小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明（包含设计费与印刷费），乙公司的收费与印刷卡片数量的关系如图2所示.

(1)、分别写出甲乙两公司的收费y（元）与印刷数量x之间的关系式.

(2)、如果你是小强，你会选择哪家公司？并说明理由.

查看试题解析
22. 如图，在等腰直角三角形ABC中， $∠ ACB = 90 ° ， AC = BC = 4$ D是AB的中点，E，F分别是AC，BC.上的点(点E不与端点A，C重合)，且 $AE = CF$ 连接EF并取EF的中点O，连接DO并延长至点G，使 $GO = OD$ ，连接DE，DF，GE，GF

(1)、求证：四边形EDFG是正方形；

(2)、直接写出当点E在什么位置时，四边形EDFG的面积最小?最小值是多少?

查看试题解析
23. 如图1，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $C (2 ， n) ， D (h ， - 1)$ )两点与x轴，y轴分别交于A、B(0，2)两点，如果 $Δ AOC$ 的面积为6.

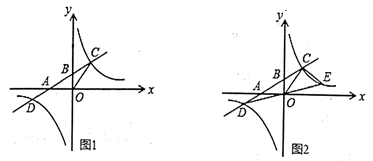(1)、求点A的坐标；

(2)、求一次函数和反比例函数的解析式；

(3)、如图2，连接DO并延长交反比例函数的图象于点E，连接CE，求点E的坐标和 $Δ COE$ 的面积

查看试题解析

班级	中位数（分）	众数（分）	平均数（分）
一班	85
二班		100	85