河南省焦作市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-07-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形的是(　　)

A、 B、 C、 D、

查看试题解析
2. 下列各式从左到右的变形中，是因式分解的为（）

A、 ${(x + y)}^{2} = x^{2} + 2 x y + y^{2}$ B、 $- 5 {(x y)}^{2} = - 5 \cdot x^{2} y^{2}$ C、 $x^{2} + 2 x + 1 = x (x + 2 + \frac{1}{x})$ D、 $x^{2} - 4 y^{2} = (x + 2 y) (x - 2 y)$

查看试题解析
3. 要使分式 $\frac{x^{2} - 16}{x + 4}$ 的值为零，则x的取值应满足（）

A、 $x \neq - 4$ B、 $x = 4$ C、 $x = - 4$ D、 $x = \pm 4$

查看试题解析
4. 如图，在 $Δ A B C$ 中，分别以点A，B为圆心，大于 $\frac{1}{2} A B$ 长为半径作弧，两弧交于点M，N，作直线MN分别交AB，AC于点D，E，连接BE，下列结论错误的是（）

A、 $A D = B D$ B、 $∠ B E C = 2 ∠ D B E$ C、 $A E = B E$ D、BE平分 $∠ C B D$

查看试题解析
5. 不等式组 ${\begin{array}{l} 2 x - 5 \geq 1 \\ 8 - 4 x < 0 \end{array}$ 中的两个不等式的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
6. 如图，E，F分别是平行四边形ABCD的边BC、AD所在直线上的点，AC，EF交于点O，请你添加一个条件，使四边形AECF是平行四边形，下列选项中不能推断四边形AECF是平行四边形的是（）

A、 $A E = C F$ B、 $E O = F O$ C、 $A E / / C F$ D、 $A F = E C$

查看试题解析
7. 如图，函数 $y = 3 x + b$ 和 $y = a x - 3$ 的图象于点 $P (- 2 ， - 5)$ ，则根据图象可得不等式 $3 x + b > a x - 3$ 的解集是（）

A、 $x > - 5$ B、 $x > - 3$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
8. 分式方程 $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 3)}$ 的解为（）

A、x＝1 B、x＝－1 C、无解 D、x＝－2

查看试题解析
9. 小明坐滴滴打车前去火车高铁站，小明可以选择两条不同路线：路线A的全程是25千米，但交通比较拥堵，路线B的全程比路线A的全程多7千米，但平均车速比走路线A时能提高60%，若走路线B的全程能比走路线A少用15分钟．若设走路线A时的平均速度为x千米/小时，根据题意，可列分式方程（）

A、 $\frac{25}{x} - \frac{32}{1.6 x}$ =15 B、 $\frac{32}{1.6 x} - \frac{25}{x}$ =15 C、 $\frac{32}{1.6 x} - \frac{25}{x}$ = $\frac{1}{4}$ D、 $\frac{25}{x} - \frac{32}{1.6 x}$ = $\frac{1}{4}$

查看试题解析
10. 如图，O是正 $Δ A B C$ 内一点， $O A = 6$ ， $O B = 8$ ， $O C = 10$ ，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：① $Δ B O^{'} A$ 可以由 $Δ B O C$ 绕点B逆时针旋转60°得到；②点O与点O′的距离为8；③ $∠ A O B = 150 °$ ；④ $S_{四边形 A O B O^{'}} = 24 + 12 \sqrt{3}$ ；其中正确的结论是（）

A、①②③ B、①③④ C、②③④ D、①②

查看试题解析

二、填空题

11. 分解因式： $x^{3} - 4 x$ =

查看试题解析
12. 不等式 $6 - 4 x \geq 3 x - 8$ 的非负整数解为.

查看试题解析
13. 如图，在 $Δ A B C$ 中， $A B = 6$ ， $A C = 4$ ，AD是角平分线，AE是中线，过点C作 $C G ⊥ A D$ 于点F，交AB于点G，连接EF，则线段EF的长为.

查看试题解析
14. 若一个多边形的每一个内角都是144°，则这个多边形的是边数为.

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ B = 90 °$ ， $A C = 10$ ， $B C = 8$ ，点D在BC上，以AC为对角线的所有 $▱ A D C E$ 中，DE的最小值是.

查看试题解析

三、解答题

16. 解方程： $\frac{1}{3 - x} = 2 - \frac{x - 2}{x - 3}$ .

查看试题解析
17. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) ⩾ 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{array}$ .

查看试题解析
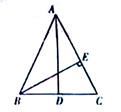
18. 先化简 $\frac{x^{2} - 4 x + 4}{x + 1} \div (\frac{3}{x + 1} - x + 1)$ ，然后从 $- 2 \leq x \leq 2$ 中选择所有合适的整数作为x的值分别代入求值.

查看试题解析
19. 如图，在∆ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.
求证：∠CBE=∠BAD.

查看试题解析
20. 如图， $Δ A B C$ 在平面直角坐标系内，三个顶点的坐标分别为 $A (- 1 ， 5)$ ， $B (- 4 ， 2)$ ， $C (- 2 ， 2)$ .

(1)、①平移 $Δ A B C$ ，使点B移动到点 $B_{1} (1 ， - 1)$ ，画出平移后的 $Δ A_{1} B_{1} C_{1}$ ，并写出点A₁ ， C₁的坐标；
②画出 $Δ A B C$ 关于原点O对称的 $Δ A_{2} B_{2} C_{2}$ ；

(2)、线段 $A A_{1}$ 的长度为.

查看试题解析
21. 如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N， $∠ A = ∠ F$ ， $∠ C = ∠ D$ .

(1)、求证：四边形BCED是平行四边形；

(2)、已知 $D E = 3$ ，连接BN，若BN平分 $∠ D B C$ ，求CN的长.

查看试题解析
22. 如图，在▱ABCD中，DE＝CE，连接AE并延长交BC的延长线于点F.

(1)、求证：△ADE≌△FCE；

(2)、若AB＝2BC，∠F＝36°，求∠B的度数．

查看试题解析
23. 近年来雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注.某商场计划购进一批A、B两种空气净化装置，每台B种设备价格比每台A种设备价格多0.7万元，花3万元购买A种设备和花7.2万元购买B种设备的数量相同.

(1)、求A种、B种设备每台各多少万元？

(2)、根据销售情况，需购进A、B两种设备共20台，总费用不高于15万元，求A种设备至少要购买多少台？

(3)、若每台A种设备售价0.6万元，每台B种设备售价1.4万元，在（2）的情况下商场应如何进货才能使这批空气净化装置售完后获利最多？

查看试题解析