浙江省衢州市2020年中考数学试题
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题(本题共有10小题,每小题3分,共30分)
-
1. 比0小1的数是( )A、0 B、-1 C、1 D、±12. 下列几何体中,俯视图是圆的几何体是( )A、
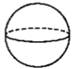 B、
B、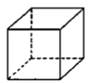 C、
C、 D、
D、 3. 计算(a²)3 , 正确的结果是( )A、a5 B、a6 C、a8 D、a94. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
3. 计算(a²)3 , 正确的结果是( )A、a5 B、a6 C、a8 D、a94. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )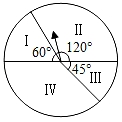 A、 B、 C、 D、5. 要使二次根式 有意义,则x的值可以是( )A、0 B、1 C、2 D、46. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 要使二次根式 有意义,则x的值可以是( )A、0 B、1 C、2 D、46. 不等式组 的解集在数轴上表示正确的是( )A、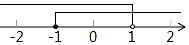 B、
B、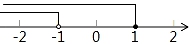 C、
C、 D、
D、 7. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
7. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( ) A、180(1-x)2=461 B、180(1+x)²=461 C、368(1-x)2=442 D、368(1+x)²=4428. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、
A、180(1-x)2=461 B、180(1+x)²=461 C、368(1-x)2=442 D、368(1+x)²=4428. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、 B、
B、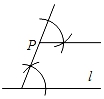 C、
C、 D、
D、 9. 二次函数y=x²的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位10. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
9. 二次函数y=x²的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位10. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共有6小题,每小题4分,共24分)
-
11. 一元一次方程2x+1=3的解是x=。12. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8,则(x-1)※x的结果为。13. 某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,则这组数据的中位数是。14. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”。已知正方形ABCD的边长为4dm,则图2中h的值为dm。
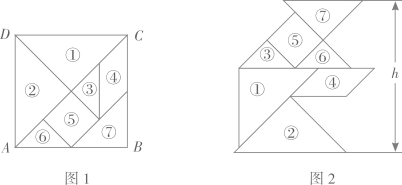 15. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M。反比例函数y= (x>0)的图象恰好经过点F,M。若直尺的宽CD=3,三角板的斜边FG=8 ,则k=。
15. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M。反比例函数y= (x>0)的图象恰好经过点F,M。若直尺的宽CD=3,三角板的斜边FG=8 ,则k=。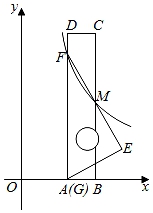 16. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。
16. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。 (1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。
(1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分。请务必写出解答过程)
-
17. 计算:|-2|+( )0- +2sin30°18. 先化简,再求值; ,其中a=3。19. 如图,在5×5的网格中,△ABC的一个顶点都在格点上。
 (1)、在图1中画出一个以AB为边的 ABDE,使顶点D,E在格点上。(2)、在图2中画出一条恰好平分△ABC周长的直线l(至少经过两个格点)。20. 某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测。根据检测结果,制成下面不完整的统计图表。
(1)、在图1中画出一个以AB为边的 ABDE,使顶点D,E在格点上。(2)、在图2中画出一条恰好平分△ABC周长的直线l(至少经过两个格点)。20. 某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测。根据检测结果,制成下面不完整的统计图表。被抽样的学生视力情况频数表
组别
视力段
频数
A
5.1≤x≤5.3
25
B
4.8≤x≤5.0
115
C
4.4≤x≤4.7
m
D
4.0≤x≤4.3
52
 (1)、求组别C的频数m的值。(2)、求组别A的圆心角度数。(3)、如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数。根据上述图表信息,你对视力保护有什么建议?21. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。
(1)、求组别C的频数m的值。(2)、求组别A的圆心角度数。(3)、如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数。根据上述图表信息,你对视力保护有什么建议?21. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。 (1)、求证:∠CAD=∠CBA。(2)、求OE的长。22. 2020年5月16日,“钱塘江诗路”航道全线开通.一艘游轮从杭州出发前往衢州,线路如图1所示。当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h;游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变)。
(1)、求证:∠CAD=∠CBA。(2)、求OE的长。22. 2020年5月16日,“钱塘江诗路”航道全线开通.一艘游轮从杭州出发前往衢州,线路如图1所示。当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h;游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变)。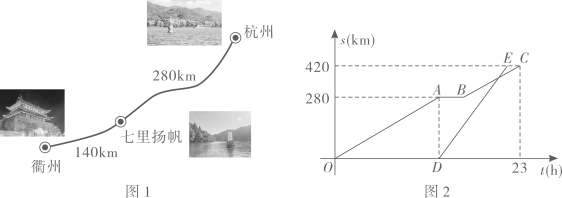 (1)、写出图2中C点横坐标的实际意义,并求山游轮在“七里扬帆”停靠的吋长。(2)、若货轮比游轮早36分钟到达衢州。问:
(1)、写出图2中C点横坐标的实际意义,并求山游轮在“七里扬帆”停靠的吋长。(2)、若货轮比游轮早36分钟到达衢州。问:①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
23. 如图1,在平面直角坐标系中,△ABC的顶点A,C分别是直线y= x+4与坐标轴的交点,点B的坐标为(-2,0)。点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF。设点D的横坐标为m,EF2为l,请探究: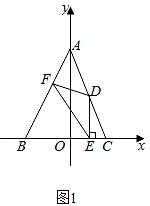
①线段EF长度是否有最小值。
②△BEF能否成为直角三角形。
小明尝试用“观察--猜想--验证--应用”的方法进行探究,请你一起来解决问题。
(1)、小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2),请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别。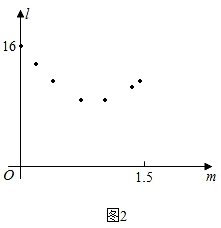 (2)、小明结合图1,发现应用二角形和函数知识能验证(1)中的猜想.请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值。(3)、小明通过观察,推理,发现△BEF能成为直角三角形。请你求出当△BEF为直角三角形时m的值。24. 【性质探究】
(2)、小明结合图1,发现应用二角形和函数知识能验证(1)中的猜想.请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值。(3)、小明通过观察,推理,发现△BEF能成为直角三角形。请你求出当△BEF为直角三角形时m的值。24. 【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E。作DF⊥AE于点H,分别交AB,AC于点F,G。
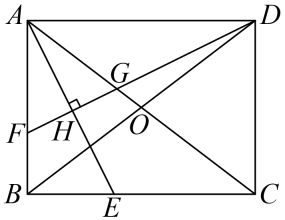 (1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】
(1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】记△DGO的面积为S1 , △DBF的面积为S2 , 当 时,求 的值。
(4)、【拓展延伸】若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF。当△BEF的面积为矩形ABCD面积的 时,请直接写出tan∠BAE的值。