浙江省温州市2020年中考数学试卷
试卷更新日期:2020-07-02 类型:中考真卷
一、选择题(本题有10小题,每小题4分,共40分.)
-
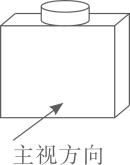
1. 数1,0, ,-2中最大的是( )A、1 B、0 C、 D、-22. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1 700 000年误差不超过1秒,数据1 700 000用科学记数法表示为( )A、17×105 B、1.7×106 C、0.17×107 D、1.7×1073. 某物体如图所示,它的主视图是( )
 A、
A、 B、
B、 C、
C、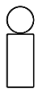 D、
D、 4. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( )
4. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( ) A、40° B、50° C、60° D、70°6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。
A、40° B、50° C、60° D、70°6. 山茶花是温州市的市花、品种多样,“金心大红”是其中的一种,某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表。株数(株)
7
9
12
2
花径(cm)
6.5
6.6
6.7
6.8
这批“金心大红”花径的众数为( )
A、6.5cm B、6.6cm C、6.7cm D、6.8cm7. 如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D。若⊙O的半径为1,则BD的长为( )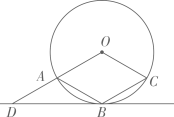 A、1 B、2 C、 D、8. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A、1 B、2 C、 D、8. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( ) A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米9. 已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y210. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q。若QH=2PE,PQ=15,则CR的长为( )
A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米9. 已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y210. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q。若QH=2PE,PQ=15,则CR的长为( )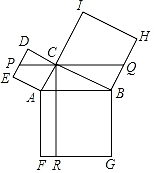 A、14 B、15 C、8 D、6
A、14 B、15 C、8 D、6二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式:m²-25=。12. 不等式组 的解为 。13. 若扇形的圆心角为45°,半径为3,则该扇形的弧长为。14. 某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生猪有头。
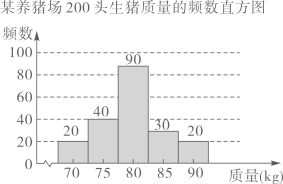 15. 点P,Q,R在反比例函数y= (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3;若OE=ED=DC,S1+S3=27,则S2的值为。
15. 点P,Q,R在反比例函数y= (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3;若OE=ED=DC,S1+S3=27,则S2的值为。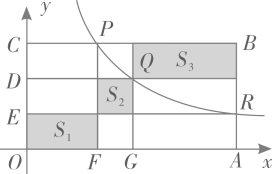 16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。
16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。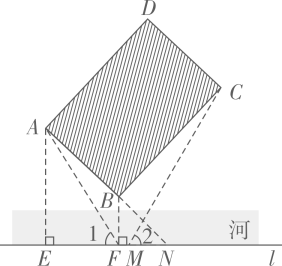
三、解答题(本题有8小题,共80分.)
-
17.(1)、计算: -|-2|+( )0-(-1)(2)、化简:(x-1)2-x(x+7)18. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE。
 (1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。19. A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示。
(1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。19. A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示。 (1)、要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量。(2)、已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元)。根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由。20. 如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合。
(1)、要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量。(2)、已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元)。根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由。20. 如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合。
注:图1,图2在答题纸上。
(1)、在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH。(2)、在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ= MN。21. 已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13)。(1)、求a,b的值。(2)、若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12-y1 , 求m的值。22. 如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是 上一点,∠ADC=∠G。 (1)、求证:∠1=∠2。(2)、点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1= ,求⊙O的半径。23. 某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进一批相同的恤衫,数量是3月份的2倍,但每件进价涨了10元。(1)、4月份进了这批T恤衫多少件?(2)、4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元。甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同。
(1)、求证:∠1=∠2。(2)、点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1= ,求⊙O的半径。23. 某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进一批相同的恤衫,数量是3月份的2倍,但每件进价涨了10元。(1)、4月份进了这批T恤衫多少件?(2)、4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元。甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同。①用含a的代数式表示b。
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值。
24. 如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合)。在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N。记QN=x,PD=y,已知y=- x+12,当Q为BF中点时,y= 。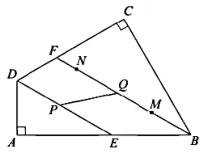 (1)、判断DE与BF的位置关系,并说明理由。(2)、求DE,BF的长。(3)、若AD=6。
(1)、判断DE与BF的位置关系,并说明理由。(2)、求DE,BF的长。(3)、若AD=6。①当DP=DF时,通过计算比较BE与BQ的大小关系。
②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值。