湖南省株洲市荷塘区2018-2019学年八年级下学期数学期末试卷
试卷更新日期：2020-07-01 类型：期末考试
一、单选题
-
1. 下列图案中，既是轴对称图形，又是中心对称图形的是( )A、
B、
C、
D、
2. 图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=( )度．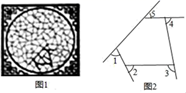
A、270° B、300° C、360° D、400°3. “学习强国”的英语“Learningpower”中，字母“n”出现的频率是（ ）A、1 B、 C、 D、24. 一次函数y=x+2的图象与x轴的交点坐标为（ ）
A、（0，2） B、（0，﹣2） C、（2，0） D、（﹣2，0）5. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O ． 下列条件不能判定平行四边形ABCD为矩形的是( )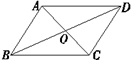
A、∠ABC＝90° B、AC＝BD C、AD＝BC ， AB∥CD D、∠BAD＝∠ADC6. 如图，∠C＝90°，AB＝12，BC＝3，CD＝4．若∠ABD＝90°，则AD的长为( )
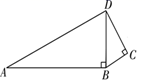A、10 B、13 C、8 D、117. 如图，在平面直角坐标系中，▱AB的顶点A、B、D的坐标分别是(0，0)，(5，0)，(2，3)，则顶点C的坐标是（ ）
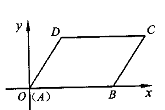A、（3，7） B、（5，3） C、（7，3） D、（8，2）8. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，ED⊥AB于D.如果∠A＝30°，AE＝6cm，那么CE等于（ ）
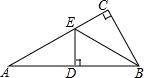A、 cm B、2cm C、3cm D、4cm9. 若把点A(－5m，2m－1)向上平移3个单位后得到的点在x轴上，则点A在( )A、x轴上 B、第三象限 C、y轴上 D、第四象限10. 小明家、食堂、图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系．根据图象，下列说法正确的是（ ）
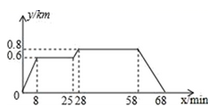A、小明吃早餐用了25min B、小明从图书馆回家的速度为0.8km/min C、食堂到图书馆的距离为0.8km D、小明读报用了30min二、填空题
-
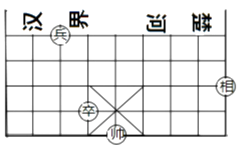
11. 点A（﹣3，0）关于y轴的对称点的坐标是 ．12. 如果正比例函数 的图象经过点（1，－2），那么k 的值等于 ．13. 如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，-1）和（-3，1），那么“卒”的坐标为。
14. 如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC的中点．若DE=5，则AB的长为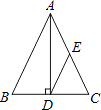
15. 抽取某校学生一个容量为150的样本，测得学生身高后，得到身高频数分布直方图如图，已知该校有学生1500人，则可以估计出该校身高位于160 cm和165 cm之间的学生大约有人.
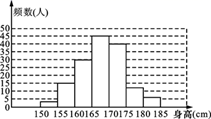16. 如图▱ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ．
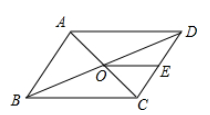17. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH ， EH=12厘米，EF=16厘米，则边AD的长是 cm.
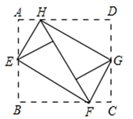18. 如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝ ，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝.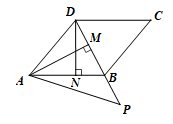
三、解答题
-
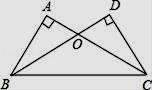
19. 如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．
20. 某校为了解八年级学生的视力情况，对八年级的学生进行了一次视力调查，并将调查数据进行统计整理，绘制出如下频数分布表和频数分布直方图的一部分．视力
频数/人
频率
4.0≤x＜4.3
20
0.1
4.3≤x＜4.6
40
0.2
4.6≤x＜4.9
70
0.35
4.9≤x＜5.2
a
0.3
5.2≤x＜5.5
10
b
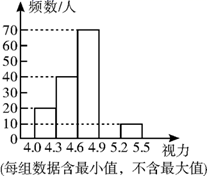(1)、在频数分布表中，a＝ ， b＝；(2)、将频数分布直方图补充完整；(3)、若视力在4.6以上(含4.6)均属正常，求视力正常的人数占被调查人数的百分比．21. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：
(1)、①作出△ABC向左平移4个单位长度后得到的△A1B1C1 ， 并写出点C1的坐标；②作出△ABC关于原点O对称的△A2B2C2 ， 并写出点C2的坐标；
(2)、已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（－4，－2），请直接写出直线l的函数解析式.22. 如图，在正方形ABCD中，AF=BE ， AE与DF相交于于点O ．
(1)、求证：△DAF≌△ABE；(2)、求∠AOD的度数．23. 如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．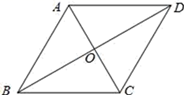
求：
(1)、两条对角线的长度；(2)、菱形的面积．24. 如图，直线m的表达式为y =﹣3x+3，且与x轴交于点B ， 直线n经过点A（4，0），且与直线m交于点C（t ， ﹣3）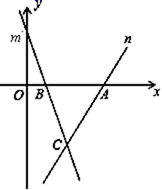
(1)、求直线n的表达式．(2)、求△ABC的面积．(3)、在直线n上存在异于点C的另一点P ， 使△ABP与△ABC的面积相等，请直接写出点P的坐标是 ．25. 已知：如图，一块Rt△ABC的绿地，量得两直角边AC=8cm，BC=6cm.现在要将这块绿地扩充成等腰△ABD ， 且扩充部分（△ADC）是以8cm为直角边长的直角三角形，求扩充等腰△ABD的周长.
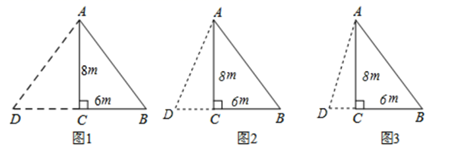(1)、在图1中，当AB=AD=10cm时，△ABD的周长为 ．(2)、在图2中，当BA=BD=10cm时，△ABD的周长为 ．(3)、在图3中，当DA=DB时，求△ABD的周长.26.
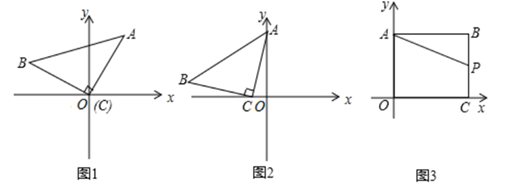(1)、操作思考：如图1，在平面直角坐标系中，等腰Rt△ACB的直角顶点C在原点，将其绕着点O旋转，若顶点A恰好落在点（1，2）处．则①OA的长为；②点B的坐标为（直接写结果）；(2)、感悟应用：如图2，在平面直角坐标系中，将等腰Rt△ACB如图放置，直角顶点C(-1，0)，点A(0，4)，试求直线AB的函数表达式；
(3)、拓展研究：如图3，在平面直角坐标系中，点B（4；3），过点B作BA y轴，垂足为点A；作BC x轴，垂足为点C，P是线段BC上的一个动点，点Q是直线 上一动点．问是否存在以点P为直角顶点的等腰Rt△APQ，若存在，请求出此时P的坐标，若不存在，请说明理由．