湖南省邵阳市邵东县2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列交通标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点M（2019，–2019）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 将函数 $y = 2 x$ 的图象向下平移3个单位，则得到的图象相应的函数表达式为（）

A、 $y = 2 x + 3$ B、 $y = 2 x - 3$ C、 $y = 2 x + 6$ D、 $y = 2 x - 6$

查看试题解析
4. 要使矩形ABCD为正方形，需要添加的条件是（　　）

A、AB=BC B、AD=BC C、AB=CD D、AC=BD

查看试题解析
5. 已知点A（-5，y₁）、B（-2，y₂）都在直线y=- $\frac{1}{2}$ x上，则y₁与y₂的关系是（　　）

A、 $y_{1} \leq y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、 $y_{1} > y_{2}$

查看试题解析
6. 如图，在△ABC中，AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）

A、2 B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
7. 如图，△ABC顶点C的坐标是（1，-3），过点C作AB边上的高线CD，则垂足D点坐标为（　　）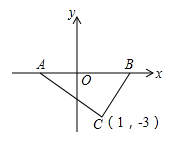

A、（1，0） B、（0，1） C、（-3，0） D、（0，-3）

查看试题解析
8. 下列说法正确的是（　　）

A、顺次连接任意一个四边形四边的中点，所得到的四边形一定是平行四边形 B、平行四边形既是中心对称图形，又是轴对称图形 C、对角线相等的四边形是矩形 D、只要是证明两个直角三角形全等，都可以用“HL”定理

查看试题解析
9. 尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；
Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．
如图是按上述要求排乱顺序的尺规作图：

则正确的配对是（）

A、①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣Ⅲ B、①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣Ⅰ C、①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣Ⅰ D、①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ

查看试题解析
10. 如图中的图象（折线ABCDE）描述了一汽车在某一直道上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系．根据图中提供的信息，给出下列说法：
①汽车共行驶了120千米；

②汽车在行驶途中停留了0.5小时；

③汽车在整个行驶过程中的平均速度为 $\frac{160}{3}$ 千米/时；

④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．

其中正确的说法有（　　）

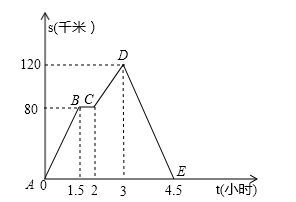A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知数据 $\sqrt[3]{4}$ ，－7， $\sqrt{2}$ ， $π$ ，－2017，其中出现无理数的频率是.

查看试题解析
12. 已知一次函数y＝2x＋b ，当x＝3时，y＝10，那么这个一次函数在y轴上的交点坐标为．

查看试题解析
13. 如图，在矩形ABCD中，已知AB=3，BC=4，则BD= ．

查看试题解析
14. 如图，平行四边形ABCD中，AC⊥AB，点E为BC边中点，AD=6，则AE的长为．

查看试题解析
15. 已知一次函数y=mx+n（m≠0）与x轴的交点为（3，0），则方程mx+n=0（m≠0）的解是x= ．

查看试题解析
16. 已知，如图，正方形ABCD的面积为25，菱形PQCB的面积为20，则阴影部分的面积为．

查看试题解析

三、解答题

17. 如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，∠CAB=60°，BD=2，求CD的长．

查看试题解析
18. 已知：如图，在▱ABCD中，E、F是对角线AC上的两点，且AE=CF．猜测DE和BF的位置关系和数量关系，并加以证明．

查看试题解析
19. 如图，已知菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E．

(1)、求证：四边形CODE是矩形；

(2)、若AB＝5，AC＝6，求四边形CODE的周长．

查看试题解析

20. 为了提高学生书写汉字的能力．增强保护汉字的意识，我区举办了“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每符合题意听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：

组别	成绩x分	频数（人数）
第1组	25≤x＜30	4
第2组	30≤x＜35	6
第3组	35≤x＜40	14
第4组	40≤x＜45	a
第5组	45≤x＜50	10

请结合图表完成下列各题：

(1)、求表中a的值；

(2)、请把频数分布直方图补充完整；

(3)、若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？

查看试题解析

21. 如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，

(1)、请在所给的网格内画出以线段AB、BC为边的菱形，并求点D的坐标；

(2)、求菱形ABCD的对角线AC的长．

查看试题解析
22. 某欢乐谷为回馈广大谷迷，在暑假期间推出学生个人门票优惠价，各票价如下：

票价种类

（A）学生夜场票

（B）学生日通票

（C）节假日通票

单价（元）

80

120

150

某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生，其中购买的B种票数是A种票数的3倍还多7张，C种票y张．

(1)、直接写出y与x之间的函数关系式；

(2)、设购票总费用为w元，求w（元）与x（张）之间的函数关系式；

(3)、为方便学生游玩，计划购买的学生夜场票不低于20张，且每种票至少购买5张，则有几种购票方案？并指出哪种方案费用最少．

查看试题解析
23. 如图所示，在△ABC中，点O是AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于F．

(1)、请猜测OE与OF的大小关系，并说明你的理由；

(2)、点O运动到何处时，四边形AECF是矩形？写出推理过程；

(3)、点O运动到何处且△ABC满足什么条件时，四边形AECF是正方形？（写出结论即可）

查看试题解析
24. 在如图所示的平面直角坐标系中，直线AB：y=k₁x+b₁与直线AD：y=k₂x+b₂相交于点A（1，3），且点B坐标为（0，2），直线AB交x轴负半轴于点C，直线AD交x轴正半轴于点D．

(1)、求直线AB的函数解析式；

(2)、若△ACD的面积为9，解不等式：k₂x+b₂＞0；

(3)、若点M为x轴一动点，当点M在什么位置时，使AM+BM的值最小？求出此时点M的坐标．

查看试题解析

票价种类	（A）学生夜场票	（B）学生日通票	（C）节假日通票
单价（元）	80	120	150