湖南省醴陵市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-07-01 类型:期末考试
一、单选题
-
1. 下列交通标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在实际生活中,我们经常利用一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )A、电动伸缩门
2. 在实际生活中,我们经常利用一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )A、电动伸缩门 B、升降台
B、升降台  C、栅栏
C、栅栏  D、窗户
D、窗户  3. 平行四边形、矩形、菱形、正方形都具有的是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直且相等4. 以下四组数中的三个数作为边长,不能构成直角三角形的是( )A、1, , B、5,12,13 C、32 , 42 , 52 D、8,15,17.5. 已知▱ABCD的周长为32,AB=4,则BC的长为 ( )
3. 平行四边形、矩形、菱形、正方形都具有的是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直且相等4. 以下四组数中的三个数作为边长,不能构成直角三角形的是( )A、1, , B、5,12,13 C、32 , 42 , 52 D、8,15,17.5. 已知▱ABCD的周长为32,AB=4,则BC的长为 ( )
A、4 B、12 C、24 D、286. 已知反比例函数 图像经过点(2,—3),则下列点中必在此函数图象上的是( )A、(2, 3) B、(1, 6) C、(—1, 6) D、(—2,—3)7. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图像大致是( )A、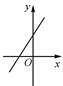 B、
B、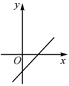 C、
C、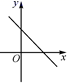 D、
D、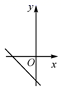 8. 点P(-2,3)到x轴的距离是( )A、2 B、3 C、
8. 点P(-2,3)到x轴的距离是( )A、2 B、3 C、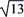 D、5
9. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
D、5
9. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )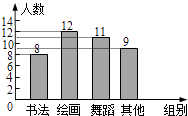 A、0.1 B、0.15 C、0.25 D、0.310. 点A(x1 , y1),B(x2 , y2),C(x3 , y3)在反比例函数y= 的图象上,若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y3
A、0.1 B、0.15 C、0.25 D、0.310. 点A(x1 , y1),B(x2 , y2),C(x3 , y3)在反比例函数y= 的图象上,若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y3二、填空题
-
11. 若一个直角三角形的两直角边长分别是1、2,则第三边长为。12. 一个多边形的内角和是它的外角和的5倍,则这个多边形的边数为。13. 在Rt△ABC中,∠ACB=90°,D为AB上的中点,若CD=5cm,则AB=cm.14. 已知菱形的两对角线长分别为6㎝和8㎝,则菱形的面积为㎝215. 在平面直角坐标系中,点P(a-1,a)是第二象限内的点,则a的取值范围是。16. 在△ABC中,点D , E分别是AB , AC的中点,且DE=3cm,则BC=cm;17. 已知如图所示,AB=AD=5,∠B=15°,CD⊥AB于C , 则CD=.
 18. 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是。
18. 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是。
三、解答题
-
19. 如图,在平面直角坐标系xOy中,A(-3,4),B(-4,1),C(-1,1).
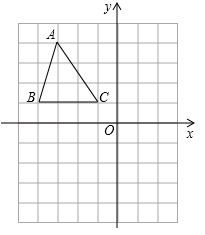 (1)、在图中作出△ABC关于x轴的轴对称图形△A′B′C′;(2)、直接写出A,B关于y轴的对称点A″,B″的坐标.20. 如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.
(1)、在图中作出△ABC关于x轴的轴对称图形△A′B′C′;(2)、直接写出A,B关于y轴的对称点A″,B″的坐标.20. 如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF. 21. 如图,在▱ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形
21. 如图,在▱ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形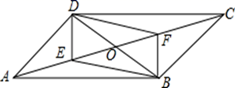 22. 某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
22. 某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
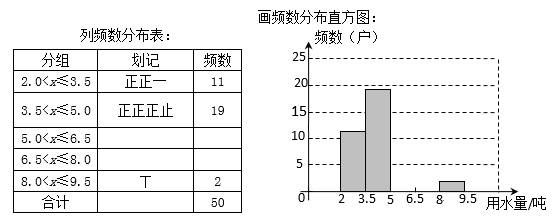 (1)、把上面的频数分布表和频数分布直方图补充完整;(2)、从直方图中你能得到什么信息?(写出两条即可)(3)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?23. 莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
(1)、把上面的频数分布表和频数分布直方图补充完整;(2)、从直方图中你能得到什么信息?(写出两条即可)(3)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?23. 莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.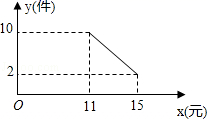 (1)、求销售量y与定价x之间的函数关系式;(2)、如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.24. 如图,在平面直角坐标系中,直线y= x+ 与反比例函数y= (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴D.
(1)、求销售量y与定价x之间的函数关系式;(2)、如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.24. 如图,在平面直角坐标系中,直线y= x+ 与反比例函数y= (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴D.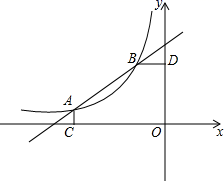 (1)、求a 、b及k的值;(2)、连接OA , OB , 求△AOB的面积.25. 如图,在△ABC中,AB=BC , BE⊥AC于点E , AD⊥BC于点D , ∠BAD=45°,AD与BE交于点F , 连接CF.
(1)、求a 、b及k的值;(2)、连接OA , OB , 求△AOB的面积.25. 如图,在△ABC中,AB=BC , BE⊥AC于点E , AD⊥BC于点D , ∠BAD=45°,AD与BE交于点F , 连接CF.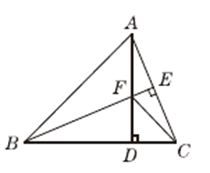 (1)、求证△ACD≌△BFD(2)、求证:BF=2AE;(3)、若CD= ,求AD的长.26. 已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
(1)、求证△ACD≌△BFD(2)、求证:BF=2AE;(3)、若CD= ,求AD的长.26. 已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1). (1)、求AB的长;(2)、擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
(1)、求AB的长;(2)、擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.