湖南省永州市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a^{6} \cdot a^{2} = a^{8}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $3 a^{2} + 2 a^{3} = 5 a^{5}$ D、 $6 a - 5 a = 1$

查看试题解析
3. 若 $3 x^{a + b} y^{2}$ 与 $4 x^{3} y^{a - b}$ 是同类项，则 $a - b$ 的值是（）

A、0 B、1 C、2 D、3

查看试题解析
4. 下列选项不是方程 $2 x - y = 5$ 的解的是（）

A、 ${\begin{matrix} x = 4 \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$

查看试题解析

5. 为了增强学生体质，学校发起评选“健步达人”活动，某同学用计步器记录自己一周（七天）每天走的步数，统计如下表：

星期	日	一	二	三	四	五	六
步数（万步）	1.3	1.0	1.2	1.4	1.3	1.1	0.9

这组数据的众数是（）

A、1.3 B、1.2 C、0.9 D、1.4

查看试题解析

6. 如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（　　）

A、 $∠ 3 = ∠ 4$ B、 $∠ 1 = ∠ 2$ C、 $∠ B = ∠ 2$ D、 $∠ D = ∠ D C E$

查看试题解析
7. $a$ ， $b$ ， $c$ 是同一平面内的三条直线，下列说法错误的是（）

A、如果 $a ∥ b$ ， $b ∥ c$ ，那么 $a ∥ c$ B、如果 $a ∥ b$ ， $b ⊥ c$ ，那么 $a ⊥ c$ C、如果 $a ⊥ c$ ， $b ⊥ c$ ，那么 $a ⊥ c$ D、如果 $a ⊥ b$ ， $b ⊥ c$ ，那么 $a ∥ c$

查看试题解析
8. 如图，将 $Δ A B C$ 绕点 $A$ 按逆时针方向旋转 $100^{\circ}$ 得到 $A B' C'$ （点 $B$ 的对应点是点 $B'$ ，点 $C$ 的对应点是点 $C'$ ），连接 $B B'$ ，若 $A C' ∥ B B'$ ，则 $∠ C' A B'$ 的度数为（）

A、 $20^{\circ}$ B、 $30^{\circ}$ C、 $40^{\circ}$ D、 $45^{\circ}$

查看试题解析
9. 现有如图所示的卡片若干张，其中A类、B类为正方形卡片，C类为长方形卡片，若用此三类卡片拼成一个长为 $a + 2 b$ ，宽为 $a + b$ 的大长方形，则需要C类卡片张数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 为节约能源，优化电力资源配置，提高电力供应的整体效益，国家实行了错峰用电.某地区的居民用电，按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多 $50 %$ ，6月份白天时段用电量比5月份白天时段用电量少 $60 %$ ，结果6月份的总用电量比5月份的总用电量多 $20 %$ ，但6月份的电费却比5月份的电费少 $10 %$ ，则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为（）

A、 $62.5 %$ B、 $50 %$ C、 $40 %$ D、 $37.5 %$

查看试题解析

二、填空题

11. 因式分 $a x^{2} - 4 a$ = ．

查看试题解析
12. 计算 ${(x^{2})}^{3}$ 的结果等于.

查看试题解析
13. 若 $x^{2} - 6 x + k$ 是完全平方式，则k的值为.

查看试题解析
14. 5名同学每周在校锻炼的时间（单位：小时）分别为：7，5，8，6，9，这组数据的中位数是.

查看试题解析
15. 如图，直线AB、CD被直线EF所截，则∠1的内错角是.

查看试题解析
16. 已知a+ $\frac{1}{a}$ =2，求a²+ $\frac{1}{a^{2}}$ = ．

查看试题解析
17. 如图，直线a平移后得到直线b，若 $∠ 1 = 70^{\circ}$ ，则 $∠ 2 - ∠ 3 =$ .

查看试题解析
18. 如图，四边形 $A B C D$ 和四边形 $C E F G$ 都是正方形，且 $B$ ， $C$ ， $E$ 三点都在同一条直线上，连接 $B D$ ， $D F$ ， $B F$ ，当 $B C = 6$ 时， $Δ D B F$ 的面积为.

查看试题解析

三、解答题

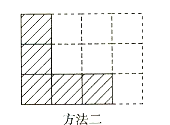
19. 如图所示，阴影部分是由5个小正方形组成的一个图形，请用两种方法分别在图中方格内涂黑2个小正方形，使它们成为轴对称图形。

查看试题解析
20. 用适当方法解下列方程组．

(1)、 ${\begin{matrix} x = 1 - y \\ 2 x - y = - 4 \end{matrix}$

(2)、 ${\begin{matrix} 2 x - 3 y = 8 \\ 4 x + 5 y = 27 \end{matrix}$ ．

查看试题解析
21. 先化简再求值： $(x + 2 y) (x - 2 y) (x^{2} - 4 y^{2})$ ，其中 $x = 2$ ， $y = - 1$ .

查看试题解析

22. 某校有甲、乙两名队员进行定点投篮比赛，他们每次各自投10个球，投篮5次，每次投篮投中个数记录如下：

队员	第1次	第2次	第3次	第4次	第5次
甲	8	7	8	9	8
乙	10	9	8	9	5

(1)、分别求出甲、乙两名队员每次投篮投中个数的平均数；

(2)、从甲、乙两名队员选择一名队员代表学校参加比赛，你会如何选择？为什么？

查看试题解析

23. 下面是某同学对多项式 $(x^{2} - 2 x) (x^{2} - 2 x + 2) + 1$ 进行因式分解的过程：
解：设 $x^{2} - 2 x = y$

原式 $= y (y + 2) + 1$     （第一步）

$= y^{2} + 2 y + 1$     （第二步）

$= {(y + 1)}^{2}$     （第三步）

$= {(x^{2} - 2 x + 1)}^{2}$     （第四步）

请问：

(1)、该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”），若不彻底，则该因式分解的最终结果为；

(2)、请你模仿上述方法，对多项式 $(x^{2} - 2 x) (x^{2} - 2 x + 2) + 1$ 进行因式分解.

查看试题解析
24. “五一”期间，部分同学随家长一同到某公园游玩，下面是购买门票时，甲同学与其爸爸的对话（如图），试根据图中的信息，解决下列问题：
票价

成人：每人80元

学生：按成人票价五折优惠

团体票：16人以上（含16人），每人按成人票价六折优惠

成人门票每张80元，学生门票五折优惠，我们一共12人，共需800元.

爸爸，等一下，让我算一算，换一种方式，购票是否可以省钱.

(1)、本次共去了几个成人，几个学生？

(2)、甲同学所说的另一种购票方式，是否可以省钱？试说明理由.

查看试题解析
25. 如图，直线 $a ∥ b$ ， $A B$ 与 $a$ ， $b$ 分别相交于点 $A$ ， $B$ ，且 $A C ⊥ A B$ ， $A C$ 交直线 $b$ 于点 $C$ .

(1)、若 $∠ 1 = 60^{\circ}$ ，求 $∠ 2$ 的度数；

(2)、若 $A C = 5$ ， $A B = 12$ ， $B C = 13$ ，求直线 $a$ 与 $b$ 的距离.

查看试题解析
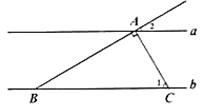26. 直线AB∥CD，点P在两平行线之间，点E. F分别在AB、CD上，连接PE，PF.尝试探究并解答：

(1)、若图1中∠1=36°，∠2=63°，则∠3=；

(2)、探究图1中∠1，∠2与∠3之间的数量关系，并说明理由；

(3)、如图2所示，∠1与∠3的平分线交于点P`，若∠2=α，试求∠EP`F的度数(用含α的代数式表示)；

(4)、如图3所示，在图2的基础上，若∠BEP $_{1}$ 与∠DFP $_{1}$ 的平分线交于点P $_{2}$ ，∠BEP $_{2}$ 与∠DFP $_{2}$ 的平分线交于点P $_{3}$ …∠BEP $_{n - 1}$ 与∠DFP $_{n - 1}$ 的平分线交于点P $_{n}$ ，且∠2=α，直接写出∠EP $_{n}$ F的度数(用含α的代数式表示).

查看试题解析