湖南省益阳市赫山区2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各图标中，是轴对称图形的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是下列哪个二元一次方程的解（）

A、 ${\begin{array}{l} x + y = 0 \\ x - y = - 1 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ x - y = 1 \end{array}$ C、 ${\begin{array}{l} x + y = 0 \\ x - y = - 2 \end{array}$ D、 ${\begin{array}{l} x + y = 0 \\ x - y = 2 \end{array}$

查看试题解析
3. 若 $a^{2} - b^{2} = 3$ ，则 ${(a + b)}^{2} \cdot {(a - b)}^{2}$ 的值是（）

A、3 B、6 C、9 D、18

查看试题解析
4. 如图， $AB ∥ CD$ ，AE平分 $∠ C A B$ 交CD于点E ，若 $∠ C = 40^{°}$ ，则 $∠ A E C$ 的度数是（）

A、 $40^{°}$ B、 $70^{°}$ C、 $110^{°}$ D、 $130^{°}$

查看试题解析
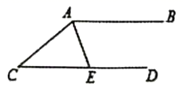5. 如图，直线a ， b被直线c所截，下列条件能使a//b的是（）

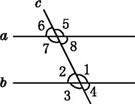A、∠1=∠6 B、∠2=∠6 C、∠1=∠3 D、∠5=∠7

查看试题解析
6. 把x²y﹣2y²x+y³分解因式正确的是

A、y（x²﹣2xy+y²） B、x²y﹣y²（2x﹣y） C、y（x﹣y）² D、y（x+y）²

查看试题解析
7. 有一组数据：3，5，5，6，7，这组数据的众数为（　　）

A、3 B、5 C、6 D、7

查看试题解析
8. 有大小两种圆珠笔，3枝大圆珠笔和2枝小圆珠笔的售价14元，2枝大圆珠笔和3枝小圆珠笔的售价11元.设大圆珠笔为x元/枝，小圆珠笔为y元/枝，根据题意，列方程组正确的是（）

A、 ${\begin{matrix} 3 x - 2 y = 11 \\ 2 x + 3 y = 14 \end{matrix}$ B、 ${\begin{matrix} 3 x + 2 y = 11 \\ 2 x + 3 y = 14 \end{matrix}$ C、 ${\begin{matrix} 14 x + 11 y = 3 \\ 2 x + 3 y = 11 \end{matrix}$ D、 ${\begin{matrix} 3 x + 2 y = 14 \\ 2 x + 3 y = 11 \end{matrix}$

查看试题解析
9. 已知a²+2a=1，则代数式2a²+4a﹣1的值为（）．

A、0 B、1 C、﹣1 D、﹣2

查看试题解析
10. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 计算 ${(- 2 x^{3} y^{2})}^{3} \cdot 4 x y^{2} =$ .

查看试题解析
12. 因式分解：6（x﹣3）+x（3﹣x）= ．

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} a x + b y = 7 \\ a x - b y = 1 \end{array}$ 的解，则a﹣b的值为．

查看试题解析
14. 如图，将 $Δ A B C$ 向右平移5cm得到 $Δ D E F$ ，如果 $Δ A B C$ 的周长是16cm，那么五边形ABEFD的周长是cm.

查看试题解析
15. 如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1=35°，则∠2的度数为．

查看试题解析
16. 已知直线 $a ∥ b ∥ c$ ，a与b的距离是2cm，b与c的距离是3cm，则a与c的距离是cm.

查看试题解析
17. 某校七年级（1）班50名同学中，13岁的有25人，14岁的有23人，15岁的有2人，则这个班同学年龄的中位数是岁.

查看试题解析
18. 已知 $a^{m} = 3$ ， $a^{n} = 2$ ，则 $a^{m + 2 n} =$ .

查看试题解析

三、解答题

19. 先化简，再求值： $(x + 2) (x - 2) - {(x - 2)}^{2}$ ，其中 $x = \frac{1}{4}$

查看试题解析
20. 如图是网格中由五个小正方形组成的图形，根据下列要求画图（涂上阴影）．

(1)、图①中，添加一块小正方形，使之成为轴对称图形，且有两条对称轴；

(2)、图②中，添加一块小正方形，使之成为轴对称图形，且只有一条对称轴（画出一个即可）.

查看试题解析
21. 给出三个多项式：a²+3ab﹣2b² ， b²﹣3ab，ab+6b² ，任请选择两个多项式进行加法运算，并把结果分解因式．

查看试题解析
22. 如图①是大众汽车的图标，图②是该图标抽象的几何图形，且AC∥BD，∠A＝∠B，试猜想AE与BF的位置关系，并说明理由．

查看试题解析

23. 某班在甲、乙两名同学中选拔一人参加学校数学竞赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：

次数	1	2	3	4	5
甲	79	86	82	85	83
乙	88	79	90	81	77

回答下列问题：

(1)、请分别求出甲、乙两同学测试成绩的平均数；

(2)、经计算知

S_{甲}^{2} = 6

，

S_{乙}^{2} = 26

，你认为选拔谁参加比赛更合适，说明理由．

查看试题解析

24. 某同学在计算3（4+1）（4²+1）时，把3写成(4﹣1)后，发现可以连续运用两数和乘以这两数差公式计算：
3（4+1）（4²+1）=（4﹣1）（4+1）（4²+1）=（4²﹣1）（4²+1）=16²﹣1=255．

请借鉴该同学的经验，计算： $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) + \frac{1}{2^{15}}$ ．

查看试题解析
25. 某企业在“蜀南竹海”收购毛竹，直接销售，每吨可获利100元，进行粗加工，每天可加工8吨，每吨可获利800元；如果对毛竹进行精加工，每天可加工1吨，每吨可获利4000元．由于受条件限制，每天只能采用一种方式加工，要求将在一月内（30天）将这批毛竹93吨全部销售．为此企业厂长召集职工开会，让职工讨论如何加工销售更合算．
甲说：将毛竹全部进行粗加工后销售；

乙说：30天都进行精加工，未加工的毛竹直接销售；

丙说：30天中可用几天粗加工，再用几天精加工后销售；

请问厂长应采用哪位说的方案做，获利最大？

查看试题解析
26. 学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．

(1)、小明遇到了下面的问题：如图 $l_{1} ∥ l_{2}$ ，点P在 $l_{1}$ 、 $l_{2}$ 内部，探究 $∠ A$ ， $∠ APB$ ， $∠ B$ 的关系．小明过点P作 $l_{1}$ 的平行线，可得到 $∠ APB$ ， $∠ A$ ， $∠ B$ 之间的数量关系是： $∠ APB =$ .

(2)、如图2，若 $AC ∥ BD$ ，点P在AC、BD外部， $∠ A$ ， $∠ B$ ， $∠ APB$ 的数量关系如何？为此，小明进行了下面不完整的推理证明.请将这个证明过程补充完整，并在括号内填上依据．过点P作 $PE ∥ AC$ ．
∴ $∠ A = ∠ APE$ （）

∵ $AC ∥ BD$ ，

∴ $BD ∥ PE$ （）

∴ $∠ B = ∠ BPE$ ，

∵ $∠ APB = ∠ BPE - ∠ APE$ ，

∴ $∠ APB =$ .（）

(3)、随着以后的学习你还会发现平行线的许多用途．如图3，在小学中我们已知道，三角形ABC中， $∠ A + ∠ B + ∠ C = 180^{°}$ ．试构造平行线说明理由.

查看试题解析