湖南省醴陵市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（　　）

A、x²+x²=x⁴ B、(x﹣y)²=x²﹣y² C、(﹣x)²•x³=x⁵ D、(x²y)³=x⁶y

查看试题解析
3. 下列说法正确的是（）

A、同旁内角相等，两直线平行 B、两直线平行，同位角互补 C、相等的角是对顶角 D、等角的余角相等

查看试题解析
4. 2019年我国部分省份发生了猪瘟疫情，经科学家检测猪瘟病毒的直径是0.000000042米，将0.000000042用科学记数法表示为（）

A、4.2×10^－⁹ B、4.2×10^－⁸ C、0.42×10^－⁸ D、42×10^－⁹

查看试题解析

5. 下表是某公司员工月收入的资料：

月收入/元	45000	18000	10000	5500	5000	3400	3300	1000
人数	1	1	1	3	6	1	11	1

能够反映该公司全体员工月收入水平的统计量是（）

A、平均数和众数 B、平均数和中位数 C、中位数和众数 D、平均数和方差

查看试题解析

6. 分式 $\frac{1}{a + 1} + \frac{1}{a (a + 1)}$ 的计算结果是（）

A、 $\frac{1}{a}$ B、 $\frac{a}{a + 1}$ C、 $\frac{1}{a + 1}$ D、 $\frac{a + 1}{a}$

查看试题解析
7. 如图，下列说法错误的是(　　)

A、因为∠BAD＋∠ADC＝180°，所以AB∥CD B、因为AB∥CD，所以∠BAC＝∠ACD C、因为∠ABD＝∠CDB，所以AD∥BC D、因为AD∥BC，所以∠BCA＝∠DAC

查看试题解析
8. 图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）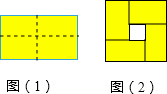

A、2mn B、（m+n）² C、（m-n）² D、m²-n²

查看试题解析
9. 如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（）

A、31° B、28° C、62° D、56°

查看试题解析
10. 已知a²+a﹣4=0，那么代数式：a²（a+5）的值是（ )

A、4 B、8 C、12 D、16

查看试题解析

二、填空题

11. 若分式 $\frac{1}{x - 5}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. ${(π - 2019)}^{0} + {(\frac{1}{2})}^{- 2}$ =。

查看试题解析
13. 如果一组数据6、7、x、10、5的众数是7，那么这组数据的平均数为。

查看试题解析
14. ${(- \frac{x}{y})}^{2} \cdot {(- 2 y)}^{3}$ =。

查看试题解析
15. 若a^m=2，aⁿ=3，则a^m+2n=.

查看试题解析
16. 若m- $\frac{1}{m}$ =3，则m²+ $\frac{1}{m^{2}}$ = ．

查看试题解析
17. 如图，已知△ABC的面积为16，BC的长为8，现将△ABC沿BC向右平移m个单位到△A′B′C′的位置。若四边形ABB′A′的面积为32，求m=。

查看试题解析
18. 如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为。

查看试题解析

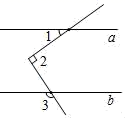
三、解答题

19. 因式分解：
①a²(x﹣y)+4b²(y﹣x)

查看试题解析
20. 先化简，再求值: ${(x - 2)}^{2} - (2 x + 1) (2 x - 1) + (3 x - 2) (x - 1)$ ,其中x=-1.

查看试题解析
21. 先化简： $(\frac{1}{x + 2} - \frac{1}{x^{2} - 4}) \div \frac{x^{2} - 6 x + 9}{x - 2}$ ，然后在－2，2，3，0中选一个合适的数代入求值。

查看试题解析

22. 为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:

班级	平均分	中位数	众数	方差
八(1)	85	b	c	d
八(2)	a	85	85	e

(1)、直接写出表中a,b,c的值：a=,b= ,c=.

(2)、求d,e的值，并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.

(3)、若“醴陵市中小学生首届诗词大会”中，各中学代表队成绩计分分两部分：现场评委记分和网络评委投票记分。且现场评委记分权数为80%，网络评委投票记分权数为20%，请计算A,B,C三所中学代表队的最终得分为多少？

	中学A	中学B	中学C
评委记分	90	80	85
网络投票记分	85	92	88

查看试题解析

23. 如图，△ABC的顶点A，B，C均在正方形网格的格点上．

(1)、画出△ABC关于直线m的对称图形△A₁B₁C₁；

(2)、画出将△ABC向下平移5个单位，再沿水平方向向左平移6个单位后，最后得到的A₂B₂C₂；

(3)、画出将△ABC绕点A顺时针旋转90°后，所得到的图形，△AB₃C₃；

查看试题解析
24. 填空并完成以下证明：
已知：点P在直线CD上，∠BAP+∠APD=180°，∠1=∠2．

求证：AB∥CD，∠E=∠F．

证明：∵∠BAP+∠APD=180°，（已知）

∴AB∥ ．（）

∴∠BAP= ．（）

又∵∠1=∠2，（已知）

∠3=﹣∠1，

∠4=﹣∠2，

∴∠3=（等式的性质）

∴AE∥PF．（）

∴∠E=∠F．（）

查看试题解析
25. 阅读材料：我们知道：若几个非负数相加得零，则这些数都必同时为零。
例如：①（a﹣1）²+（b+5）²=0，我们可以得：（a﹣1）²=0，（b+5）²=0，∴a=1，b=-5．

②若m²-4m+n²+6n+13=0，求m、n的值．

解：∵m²-4m+n²+6n+13=0，

∴（m²﹣4m+4)+(n²+6n+9)=0(我们将13拆成4和9，等式左边就出现了两个完全平方式）

∴(m﹣2)²+(n+3)²=0，

∴(m﹣2)²=0，(n+3)²=0，

∴ n=2，m=-3．

根据你的观察，探究下面的问题：

(1)、a²﹣4a+4+b²=0，则a= ． b= ．

(2)、已知x²+2xy+2y²－6y+9=0，求x^y的值．

(3)、已知a、b（a≠b）是等腰三角形的边长，且满足2a²+b²﹣8a﹣6b+17=0，求三角形的周长。

查看试题解析
26. 已知：∠A=（90+x）°，∠B=（90﹣x）°，∠CED=90°，射线EF∥AC，2∠C﹣∠D=m.

(1)、判断AC与BD的位置关系，并说明理由．

(2)、如图1，当m=30°时，求∠C、∠D的度数．

(3)、如图2，求∠C、∠D的度数（用含m的代数式表示）．

查看试题解析