广东省汕头市龙湖区2020年中考数学模拟试卷

试卷更新日期：2020-07-01 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，是无理数的一项是（）

A、0 B、﹣1 C、0.101001 D、 $\sqrt[3]{9}$

查看试题解析
2. 由5个大小相同的正方体组成的几何体如图所示，其主视图是（）

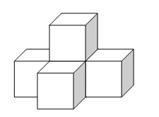A、 B、 C、 D、

查看试题解析
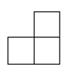3. 下列运算正确的是（　　）

A、2x+3y=5xy B、5x²•x³=5x⁵ C、4x⁸÷2x²=2x⁴ D、（﹣x³）²=x⁵

查看试题解析
4. 如图由正三角形和正方形拼成的图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 以方程组 ${\begin{matrix} y = - x + 2 \\ y = x - 1 \end{matrix}$ 的解为坐标的点（x，y）在平面直角坐标系中的位置是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
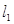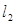6. 如图，直线、被直线所截，下列选项中不能得到 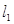∥ 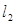的是（）

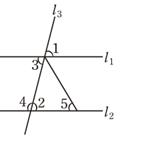A、∠1＝∠2 B、∠2＝∠3 C、∠3＝∠5 D、∠3+∠4＝180°

查看试题解析
7. 甲、乙、丙三个游客团的年龄的方差分别是 $S_{甲}^{2}$ ＝1.4， $S_{乙}^{2}$ ＝18.8， $S_{丙}^{2}$ ＝2.5，导游小方最喜欢带游客年龄相近的团队，若在这三个游客团中选择一个，则他应选（）

A、甲队 B、乙队 C、丙队 D、哪一个都可以

查看试题解析
8. 如图， $P A$ ， $P B$ 切⊙O于点 $A$ ， $B$ ，点 $C$ 是⊙O上一点，且∠P=36°，则∠ACB=（）

A、 $54 °$ B、 $72 °$ C、 $108 °$ D、 $144 °$

查看试题解析
9. 如图，若 $a b$ <0，则正比例函数 $y = a x$ 与反比例函数 $y = \frac{b}{x}$ 在同一坐标系的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
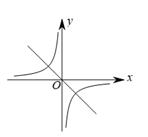10. 如图，在正方形ABCD中，E，F分别为BC，CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长于点Q，下列结论正确的有（）个．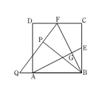

①AE⊥BF； ②QB＝QF； ③ $\frac{A G}{F G} = \frac{4}{3}$ ； ④S_ECPG＝3S_△_BGE

A、1 B、4 C、3 D、2

查看试题解析

二、填空题

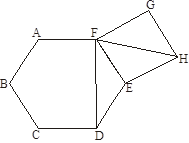
11. 4的算术平方根是 9的平方根是 64的立方根是

查看试题解析
12. 我国首部国产科幻灾难大片《流浪地球》于2019年2月5日在我国内地上映，自上映以来票房累计突破46.7亿元，将46.7亿元用科学记数法表示为

查看试题解析
13. 因式分解： $m^{3} n - 9 m n =$

查看试题解析
14. 若 $\sqrt{a - 3} + {(b + 4)}^{2} = 0$ ，那么点（a，b）关于原点对称点的坐标是

查看试题解析
15. 如图，在正六边形 $A B C D E F$ 的外侧，作正方形 $E F G H$ ，则∠DFH 的度数为

查看试题解析
16. 如图，两个直角三角板ABC与CDE按如图所示的方式摆放，其中∠B=∠D=30°，∠ACB=∠ECD=30°， $A C = C E = \sqrt{3}$ ，且 $A$ 、 $C$ 、 $D$ 共线，将 $Δ D C E$ 沿DC方向平移得到 $Δ D^{'} C^{'} E^{'}$ ，若点 $E^{'}$ 落在 $A B$ 上，则平移的距离为．

查看试题解析
17. 如图，AC⊥BC，AC=BC=2，以BC为直径作半圆，圆心为O，以点C为圆心，BC为半径作弧AB，过点O作AC的平行线交两弧于点D、E，则阴影部分的面积是.

查看试题解析

三、解答题（一）

18. ${(\sqrt{3} - 2)}^{0} + {(- \frac{1}{4})}^{- 1} + 4 \cos 30^{\circ} - | 4 - 2 \sqrt{3} |$

查看试题解析
19. 化简求值： $\frac{x + 1}{x^{2} - 2 x + 1} \div (1 + \frac{2}{x - 1})$ ，其中 $x = \sqrt{3}$

查看试题解析
20. 如图，△ABC中，∠C=90°，∠A=30°．

(1)、用直尺和圆规作AB边上的垂直平分线DE，交AC于点D，交AB于点E．（保留作图痕迹，
不要求写作法和证明）

(2)、在（1）的条件下，连接BD，求证：DE=CD

查看试题解析

四、解答题（二）

21. 为了庆祝中华人民共和国成立70周年，某市决定开展“我和祖国共成长”主题演讲比赛，某中学将参加本校选拔赛的40名选手的成绩（满分为100分，得分为正整数且无满分，最低为75分）分成五组，并绘制了下列不完整的统计图表．

分数段	频数	频率
74.5～79.5	2	0.05
79.5～84.5	m	0.2
84.5～89.5	12	0.3
89.5～94.5	14	n
94.5～99.5	4	0.1

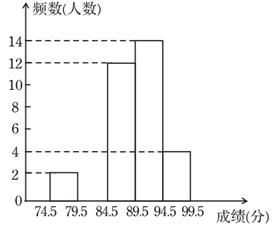(1)、表中m＝， n＝；

(2)、请在图中补全频数直方图；

(3)、甲同学的比赛成绩是40位参赛

选手成绩的中位数，据此推测他的成绩落在分数段内；

(4)、选拔赛中，成绩在94.5分以上的选手，男生和女生各2人，学校从中随机确定2名选手参加全市决赛，恰好是一名男生和一名女生的概率是．

查看试题解析

22. 如图所示，要在某东西走向的A、B两地之间修一条笔直的公路，在公路起点A处测得某农户C在A的北偏东68°方向上．在公路终点B处测得该农户C在点B的北偏西45°方向上．已知A、B两地相距2400米．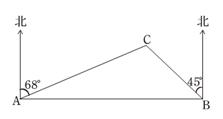

(1)、求农户C到公路 $A B$ 的距离；（参考数据：sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$ ）

(2)、现在由于任务紧急，要使该修路工程比原计划提前4天完成，需将该工程原定的工作效率提高20%，求原计划该工程队毎天修路多少米？

查看试题解析
23. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC、BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．连接OE．

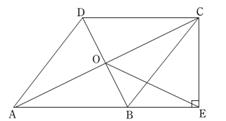(1)、求证：四边形ABCD是菱形；

(2)、若AB＝ $\sqrt{5}$ ．OE＝2，求线段CE的长．

查看试题解析

五、解答题（三）

24. 如图，在⊿ABC中，AB=BC，以BC为直径的⊙O交AC于点D，过D作DE⊥AB，DF⊥BC，垂足分别为E、F，

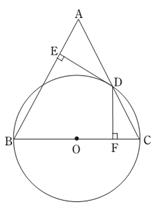(1)、求证： $E D$ 是⊙O的切线；

(2)、求证： $D E^{2} = B F \cdot A E$ ；

(3)、若 $D F = 3 \sqrt{5}$ ， $\cos A = \frac{2}{3}$ ，求⊙O的直径．

查看试题解析
25. 如图，抛物线 $y = - \frac{1}{2} x^{2} + \frac{5}{2} x - 2$ 与轴交于A、B两点，与 $y$ 轴交于点C，四边形OBHC为
矩形，CH的延长线交抛物线于点D（5，－2），连接

BC、AD．

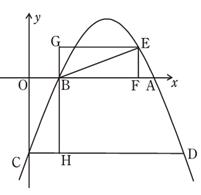(1)、将矩形OBHC绕点B按逆时针旋转90°后，再沿轴对折到矩形GBFE（点C与点E对应，点O与点G对应），求点E的坐标；

(2)、设过点E的直线交AB于点P，交CD于点Q．
①当四边形PQCB为平行四边形时，求点P的坐标；

②是否存在点P，使直线PQ分梯形ADCB的面积为1∶3两部分？若存在，求出点P坐标；若不存在，请说明理由．

查看试题解析