广东省汕头市澄海区2020年中考数学模拟试卷

试卷更新日期：2020-07-01 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个实数中，最大的实数是（）

A、 $| - \sqrt{3} |$ B、-2 C、0 D、 $\sqrt{2}$

查看试题解析
2. 中国倡导的“一带一路”建设将促进世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为44亿人，这个数据用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、4.4×10¹⁰

查看试题解析
3. 下列轴对称图形中只有一条对称轴的是（）

A、 B、 C、 D、

查看试题解析
4. 为了解小区居民使用共享单车的情况，某研究小组随机采访该小区的10位居民，得到这10位居民一周内使用共享单车的次数分别为：17，12，15，20，17，9，7，26，17，9．这组数据的众数是（）

A、17 B、7 C、16 D、15

查看试题解析
5. 下面计算正确的是（）

A、 $3 + \sqrt{3} = 3 \sqrt{3}$ B、 $\sqrt{27} \div \sqrt{3} = 3$ C、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{5}$ D、 $\sqrt{4} = \pm 2$

查看试题解析
6. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则实数 $k$ 的取值范围是（）

A、 $k > - 1$ B、 $k \geq - 1$ C、 $k > - 1$ 且 $k \neq 0$ D、 $k \geq - 1$ 且 $k \neq 0$

查看试题解析
7. 实数a，b，c，d在数轴上的对应点的位置如图所示，则下列结论正确的是（）

A、 $a c > 0$ B、 $| b | < | c |$ C、 $a < - d$ D、 $b + d > 0$

查看试题解析
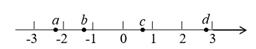8. 如图，直线 $l_{1}$ ∥ $l_{2}$ ，AB=BC，CD⊥AB于点D，若∠DCA=25°，则∠1的度数为（）

A、70° B、65° C、60° D、55°

查看试题解析
9. 如图，已知菱形OABC的顶点C的坐标为（3，4）．顶点A在 $x$ 轴的正半轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过顶点B，则 $k$ 的值为（）

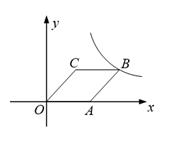A、12 B、20 C、24 D、32

查看试题解析
10. 如图，在边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH＝DF，连接AH、FH，FH与AC交于点M．下面结论：①FH＝2BH；②AC⊥FH；③DF＝1；④ EG²＝FG•DG．其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 9的平方根是，使分式 $\frac{1}{x + 1}$ 有意义的x的取值范围是．

查看试题解析
12. 分解因式： $4 x^{2} - 1 =$ ．

查看试题解析
13. 如图，要测量小河两岸相对的两点P、A的距离，可以在小河边取PA的垂线PQ上的一点G，测得PG= $50 \sqrt{3}$ 米，∠PGA=30°，则小河宽PA为米．

查看试题解析
14. 一组按规律排列的式子： $a^{2}$ ， $\frac{a^{4}}{3}$ ， $\frac{a^{6}}{5}$ ， $\frac{a^{8}}{7}$ ，……．按这样的规律，第 $n$ （ $n$ 为正整数）个式子为．

查看试题解析
15. 我国古代数学著作《算法统宗》中记载了“绳索量竿”问题，其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．求绳索和竿的长度．设绳索长x尺，竿长y尺，可列方程组为．

查看试题解析
16. 如图，AB是⊙O的一条弦，P是⊙O上一动点（不与点A，B重合），M，N分别是BP，AB的中点．若AB=4，∠APB=30°，则MN长的最大值为．

查看试题解析
17. 如图，在矩形ABCD中，AB＝2，AD＝4，点E在边BC上，把△DEC沿DE翻折后，点C落在C′处．若△ABC′恰为等腰三角形，则CE的长为．

查看试题解析

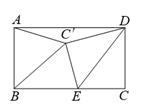
三、解答题（一）

18. 计算： $| - \sqrt{3} | + {(2020 - π)}^{0} - 2 \cos 30^{\circ} - {(- \frac{1}{3})}^{- 1}$ ．

查看试题解析
19. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (\frac{2}{a - 1} + 1)$ ，其中 $a = \sqrt{2} + 1$ ．

查看试题解析
20. 如图，在△ABC中，AB=AC，点M在BA的延长线上．

(1)、按下列要求作图，并在图中标明相应的字母（尺规作图，保留作图痕迹，不要求写作法和证明）；
①作∠MAC的平分线AN；②在AN上截取AD=BC，连结CD．

(2)、在（1）的条件下，判断四边形ABCD的形状，并证明你的结论．

查看试题解析

四、解答题（二）

21. 某学校为了增强学生体质，丰富课余生活，决定开设以下体育课外活动项目：A．篮球，B．乒乓球，C．羽毛球，D．足球．为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

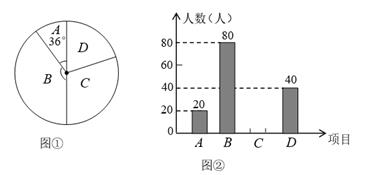(1)、这次被调查的学生共有人，在扇形统计图中B区域的圆心角度数为；

(2)、请你将条形统计图补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，学校决定从这四名同学中任选两名参加市乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

查看试题解析
22. 如图，矩形AEHC是由三个全等矩形拼成的，AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N，设△BPQ、△DKM、△CNH的面积依次为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ．

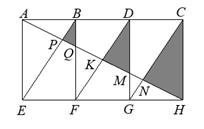(1)、求证：△BPQ∽△DKM∽△CNH；

(2)、若 $S_{1} + S {}_{3}= 40$ ，求 $S_{2}$ 的值．

查看试题解析
23. 小明骑自行车从家中前往地铁一号线的B站，与此同时，一列地铁从A站开往B站.3分钟后，地铁到达B站，小明离B站还有1800米．已知A、B两站间的距离和小明家到B站的距离恰好相等，这列地铁的平均速度是小明骑车速度的4倍．

(1)、求小明骑车的平均速度；

(2)、如果此时另有一列地铁需8分钟到达B站，且小明骑车到达B站后还需2分钟才能走到地铁站台候车，他要想乘上这趟地铁，骑车的平均速度至少应提高多少？（假定这两列地铁的速度相同）

查看试题解析

五、解答题（三）

24. 如图，已知在Rt△ABC中，∠C=90°，以BC为直径的⊙O交斜边AB于点E，若D是AC的中点，连结DE．

(1)、求证：DE为⊙O的切线；

(2)、若 $D E = \frac{3}{2}$ ， $\tan ∠ A B C = \frac{3}{4}$ ，求⊙O的半径长；

(3)、在（2）的条件下，过点A作⊙O的另一条切线，切点为F，过点F作FG⊥BC，垂足为H，且交⊙O于G点，连结AO 交CF于点P．求线段FG的长度．

查看试题解析
25. 如图，已知在矩形ABCD中，AD=10cm，AB=4cm，动点P从点A出发，以2cm/s的速度沿AD向终点D移动，设移动时间为 $t$ （s）．连接PC，以PC为一边作正方形PCEF，连接DE、DF．

(1)、求正方形PCEF的面积（用含 $t$ 的代数式来表示，不要求化简），并求当正方形PCEF的面积为25 cm²时 $t$ 的值；

(2)、设△DEF的面积为 $S$ （cm²），求 $S$ 与 $t$ 之间的函数关系式，并求当 $t$ 为何值时？△DEF的面积取得最小值，这个最小值是多少？

(3)、求当 $t$ 为何值时？△DEF为等腰三角形．

查看试题解析