广东省汕头市潮阳区2020年中考数学模拟试卷
试卷更新日期:2020-07-01 类型:中考模拟
一、选择题
-
1. -2020的倒数是( )A、2020 B、 C、- D、
 2020
2. 四个数0,π,-1, , 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个3. 已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )A、6 B、7 C、8 D、94. 下列运算正确的是( )A、(a2)3=a5 B、(a-b)2=a2-b2 C、 D、5. 下列图形中,主视图为①的是( )
2020
2. 四个数0,π,-1, , 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个3. 已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )A、6 B、7 C、8 D、94. 下列运算正确的是( )A、(a2)3=a5 B、(a-b)2=a2-b2 C、 D、5. 下列图形中,主视图为①的是( ) A、
A、 B、
B、 C、
C、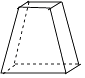 D、
D、 6. 已知一组数据45,51,54,52,45,44,则这组数据的众数、中位数分别为( )A、45,48 B、44,45 C、45,51 D、52,537. 已知 、 是一元二次方程 的两个根,则 等于( )A、4 B、 1 C、
6. 已知一组数据45,51,54,52,45,44,则这组数据的众数、中位数分别为( )A、45,48 B、44,45 C、45,51 D、52,537. 已知 、 是一元二次方程 的两个根,则 等于( )A、4 B、 1 C、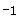 D、
D、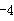 8. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,
8. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
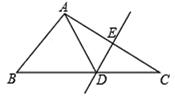 A、50° B、70° C、75° D、80°9. 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A、50° B、70° C、75° D、80°9. 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )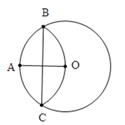 A、 B、 C、 D、10. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H。给出下列结论:
A、 B、 C、 D、10. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H。给出下列结论: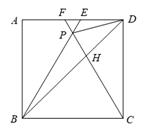
①△ABE≌△DCF ②∠PDF=15° ③ ④
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
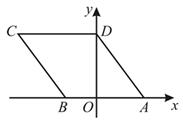
11. 将数0.000092用科学记数法表示为。12. 因式分解:2x2﹣8= .13. 分式方程 =1的解是 .14. 一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为元。15. 如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是。
 16. 观光塔是某市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°。已知楼房高AB是45m,根据以上观测数据可求观光塔的高CD是m。
16. 观光塔是某市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°。已知楼房高AB是45m,根据以上观测数据可求观光塔的高CD是m。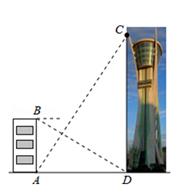 17. 如图,已知A1 , A2 , A3 , …An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,
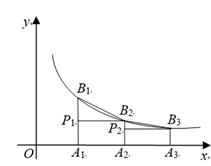
17. 如图,已知A1 , A2 , A3 , …An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1 , A2 , A3 , …An作x轴的垂线交反比例函数y= (x>0)的图象于点B1 , B2 , B3 , …Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2……,记△B1P1B2的面积为S1 , △B2P2B3的面积为S2……,△B6P6B7的面积为S6 , 则S1+S2+S3+…+S6=。
三、解答题(一)
-
18. 计算:19. 先化简 ,然后从﹣2,﹣1,0,1中选择一个适当的数代入求值。20. 如图,已知△ABC,∠ACB=90°
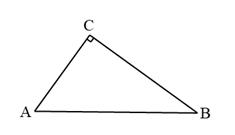 (1)、求作AB边上的高CD。(尺规作图,保留作图痕迹,不写作法)(2)、若AD=2,BD=4,求高CD的长。
(1)、求作AB边上的高CD。(尺规作图,保留作图痕迹,不写作法)(2)、若AD=2,BD=4,求高CD的长。四、解答题(二)
-
21. 某中学决定开设A:实心球。B:立定跳远,C:跳绳,D:跑步四种活动项目。为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图。请结合图中的信息解答下列问题:
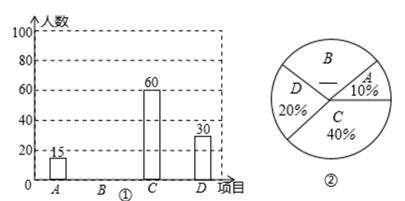 (1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生。现从这5名学生中任意抽取2名学生。请用画树状图或列表的方法,求出刚好抽到同性别学生的概率。22. 某地2018年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2020年投入资金比2018年投入资金多投入1600万元。(1)、从2018年到2020年,该地投入异地安置资金的年平均增长率为多少?(2)、在2020年异地安置的具体实施中,该地计划投入资金不低于360万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房360天计算,求2020年该地至少有多少户享受到优先搬迁租房奖励。23. 如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB。
(1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生。现从这5名学生中任意抽取2名学生。请用画树状图或列表的方法,求出刚好抽到同性别学生的概率。22. 某地2018年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2020年投入资金比2018年投入资金多投入1600万元。(1)、从2018年到2020年,该地投入异地安置资金的年平均增长率为多少?(2)、在2020年异地安置的具体实施中,该地计划投入资金不低于360万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房360天计算,求2020年该地至少有多少户享受到优先搬迁租房奖励。23. 如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB。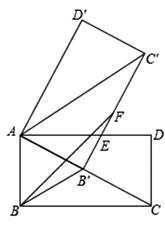 (1)、求证:BB′=FB′;(2)、求∠FBB′的度数;(3)、已知AB=4,求△BFB′面积。
(1)、求证:BB′=FB′;(2)、求∠FBB′的度数;(3)、已知AB=4,求△BFB′面积。五、解答题(三)
-
24. 如图,△ABC内接于⊙O,且AB为⊙O的直径。∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F。
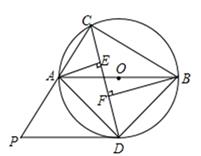 (1)、求证:EF+AE=BF;(2)、求证:△PDA∽△PCD;(3)、若AC=6,BC=8,求线段PD的长。25. 如图,一次函数y=﹣4x﹣4的图象与x轴、y轴分别交于A、C两点,抛物线y= 的图象经过A、C两点,且与x轴交于点B。
(1)、求证:EF+AE=BF;(2)、求证:△PDA∽△PCD;(3)、若AC=6,BC=8,求线段PD的长。25. 如图,一次函数y=﹣4x﹣4的图象与x轴、y轴分别交于A、C两点,抛物线y= 的图象经过A、C两点,且与x轴交于点B。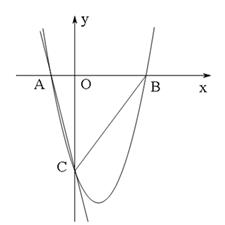 (1)、求抛物线的函数表达式;(2)、在抛物线的对称轴上找一点E,使点E到点A的距离与到点C的距离之和最小,求出此点E的坐标;(3)、作直线MN平行于x轴,分别交线段AC、BC于点M、N。问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,
(1)、求抛物线的函数表达式;(2)、在抛物线的对称轴上找一点E,使点E到点A的距离与到点C的距离之和最小,求出此点E的坐标;(3)、作直线MN平行于x轴,分别交线段AC、BC于点M、N。问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由。