山东省新泰市2020年中考数学一模试卷
试卷更新日期：2020-07-01 类型：中考模拟
一、选择题
-
1. 在-1，0，- ，-π这四个数中，最小的数是（ ）A、0 B、- π C、- D、-12. 下列运算正确的是（ ）A、x²+x²=x4 B、3a3·2a²=6a6 C、(-a2)3÷a3=-a2 D、-2x-²=3. 如图，通过折纸可以得到好多漂亮的图案，观察下列用纸折叠成的图案，其中轴对称图形和中心对称图形的个数分别是（ ）
A、3，1 B、3，0 C、3，2 D、1，34. 【海外网5月14日|战疫全时区】发布的实时统计数据显示，截至北京时间5月14日6时30分，全球累计确诊新冠肺炎病例4330982例，累计死亡295671例．数据433万用科学记数法表示为（ ）A、4.33×107 B、4.33x106 C、4.33×105 D、43.3×1065. 如图，将一个矩形纸片ABCD，沿着BE折叠，使C、D点分别落在点C1 ， D2处，若∠C1BA=40°，则∠ABE的度数为（ ）
A、15° B、20° C、25° D、30°6. 甲、乙二人在相同条件下各射靶10次，每次射靶成绩如图所示，经计算得： =1，S甲2=1.2，S乙2=5.8，则下列结论中正确的个数是（ ）①甲、乙的总环数不相等；
②甲的成绩稳定；
③甲、乙的众数相同
A、0 B、1 C、2 D、37. 已知关于x的不等式组 恰好有两个整数解，则实数a的取值范围是（ ）A、-4≤a<-3 B、-4<a≤-3 C、-4≤a≤-3 D、-4<a<-38. 如图，轮船在A处观测灯塔C位于北偏西70°方向上，轮船从A处以每小时40海里的速度沿南偏西50°方向匀速航行，1小时后到达码头B处，此时，观测灯塔C位于北偏西25°方向上，则灯塔C与码头B的距离是（ ）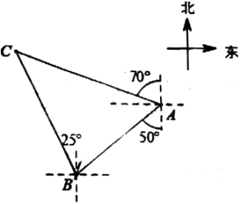
A、20 海里 B、10 海里 C、20 海里 D、10 海里9. 若一个圆锥的底面半径为2cm，高为4 cm，则圆锥的侧面展开图中圆心角的度数为（ ）A、80° B、100° C、120° D、150°10. 在同一坐标系中，二次函数y=ax2+bx与一次函数y=bx-a的图象可能是（ ）A、
B、
C、
D、
11. 如图，在△ABC中，以BC为直径的⊙O，又AB的延长线于点D，交AC于点E，连接OD，OE。若∠A=40°，则∠DOE的度数为（ ）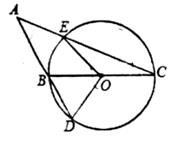
A、140° B、100° C、50 D、80°12. 如图，已知直线y= x-3与x轴、y轴分别交于A、B两点，P是以C(0，1)为圆心，1为半径的圆上一动点，连结PA、PB。则△PAB面积的最大值是（ ）
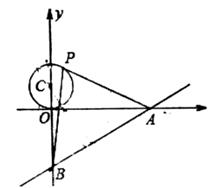A、8 B、 C、12 D、二、填空题
-
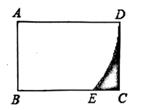
13. 已知x=1是关于x的一元二次方程(1-k)x²+k²x-1=0的根，则常数k的值为。14. 我国古代数学著作《九章算术》中记载：“今有大器五小器一容九斛，大器一小器五容三斛。问大小器各容几何。”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒9斛(斛，音hu，是古代的一种容量单位)。1个大桶加上5个小桶可以盛酒3斛，问1个大桶和1个小桶分别可以盛斛酒。15. 如图，矩形ABCD中，AB=1，AD= ，以AD的长为半径的OA交BC于点E，
则图中阴影部分的面积为。
16. 如图，抛物线y=ax²+c与直线y=mx+n交于A(-1，p)，B(3，q)两点，则不等式ax²-mx+c<n的解集是。
17. 在直角坐标系中，直线y=x+1与y轴交于点A，按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2……， 点A1、A2、A3…在直线y=x+1上，点C1、C2、C3…在x轴上，图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn ， 则S2020的值为。
18. 如图，正方形ABCD和正方形CE FG中，点D在CG上，BC=2，CE=3，H是AF的中点，EH与CF交于点O，则HE的长为。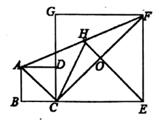
三、解答题
-
19. 先化简，再求值： ，其中x的值是方程x²-2x-3=0的解。20. 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况，进行了统计调查。随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类)并将调查结果绘成如下不完整的统计图。根据两图提供的信息，回答下列问题：
(1)、最喜欢娱乐类节目的有人，图中x=；(2)、请补全条形统计图；(3)、根据抽样调查结果，若该校有2000名学生，请你估计该校有多少名学生最喜欢娱乐类节目；(4)、在全班同学中，有甲、乙、丙、 丁等同学最喜欢体育类节目，班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛，请用列表法或树状图求同时选中甲、乙两同学的概率。21. 如图，一次函数y=x+4的图象与反比例函数y= (k为常数且k≠0)的图象交于A(-1，a)，B两点，与x轴交于点C。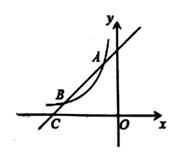
(1)、求a，k的值及点B的坐标；(2)、若点P在x轴上，且S△ACP= S△BOC ， 求出点Ｐ的坐标。22. 某水果店第一次用1200元购进一批大樱桃，很快售完；又用2500元购进第二批大樱桃，所购公斤数是第一批的2倍，但进价比第一批每公斤多了5元。(1)、求第一批大樱桃每公斤进价多少元？(2)、若以每公斤150元的价格销售第二批大樱桃，售出80%后，为了尽快售完，决定打折促销，要使第二批大樱桃的销售利润不少于320元，剩余的大樱桃每公斤售价至少打几折(利润=售价-进价)？23. 如图，在△ABC中，AD是BC边上的中线，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F。
(1)、求证：△FCD∽△ABC；(2)、过点A作AM⊥BC于点M，求DE：AM的值；(3)、若S△FCD=10，BC=16，求DE的长。24. 在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，4)，C(2，0)三点。
(1)、求抛物线的解析式；(2)、若点Ｍ为第三象限内抛物线上一动点， 点M的横坐标为m，△AMB的面积为S，求S关于m的函数关系式，并求出S的最大值。(3)、若点P是抛物线上的动点，点Q是直线y=-x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Ｑ的坐标。25. 已知四边形ABCD和四边形CEFG都是正方形， 且AB>CE。
(1)、如图1，连接BG、DE．求证：BG=DE；(2)、如图2，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD，BG=BD。求∠CDE的度数；(3)、在(2)的条件下，当正方形ABCD的边长为2 时， 请直接写出正方形CEFG的边长。