山东省青岛市平度市2020年中考数学一模（期中）试卷
试卷更新日期：2020-07-01 类型：中考模拟
一、选择题
-
1. 的相反数是（ ）A、 B、- C、± D、2. 下列图案中是中心对称图形，但不是轴对称图形的是（ ）A、
B、
C、
D、
3. 某气象站记录半月(十五天)内的最高气温(℃)情况如下：最高气温(℃)
17
18
20
21
22
天数
1
3
2
5
4
则这半月最高气温的众数、中位数分别是（ ）
A、21℃、21℃ B、22℃、20℃ C、21℃、20℃ D、22℃、21℃4. 计算(-2x2)3-x9÷x3的结果是（ ）A、7x6 B、-8x6-x3 C、-8x3-x6 D、-9x65. 如图，在平面直角坐标系中，△OAB与△OA'B'位似，位似中心为原点O，其中点A、B的对应点分别为点A'、B'，若△OAB的边上有一点P(m，n)，则点P在△OA'B'上的对应点P'的坐标为（ ）
A、(2m，2m) B、( m， n) C、(-2m，-2m) D、(- m，- n)6. 如图，点B为线段AD上一点，分别以AB和BD为边在线段AD的同侧作两个等边三角形，得到△ABC和△BDE，连接AE、CD，交点为O，则∠AOD的度数为（ ）
A、105° B、120° C、135° D、150°7. 如图，AC为⊙O的弦，AB为⊙O的直径，过点C作⊙O的切线交AB的延长线于点D，点E为⊙O上一点，若∠BEC=34°，则∠ADC的度数为（ ）
A、20° B、22° C、24° D、30°8. 二次函数y=ax2+bx+c(a≠0)的图象如图所示，下列结论：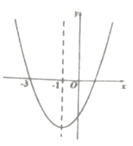
①2a+b=0；
②方程ax2+bx+c=0(a#0)有两个实数根，分别为x1=-3，x2=1；
③4a-2b+c<0；
④一次函数y= x+b的图象不经过第三象限。
其中正确的个数为（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 计算： =。10. 2020年3月11日，全国绿化委员会办公室发布《2019年中国国土绿化状况公报》显示，2019年我国国土绿化工作取得新成绩，全年共完成造林7067000公顷。将数据7067000用科学记数法表示为。11. 已知二次函数y=x²-x+k-2的图象与一次函数y=3x+2的图象有交点，则k的取值范围是。12. 如图， 将边长为 的正方形ABCD绕点C按顺时针方向旋转到FECG的位置，使得点D落在对角线CF上，EF与AD相交于点H，则HD=。
13. 如图，在△OBC中，OB=OC，∠BOC=120°，以点O为圆心，半径为2cm的圆与三边分别相交于D、E、F三点，则图中阴影部分的面积是cm²。
14. 为了致敬抗疫一线最美逆行者，小明用棱长为1的小立方块粘接成了一个如图所示的几何体．从它的每一个面看都有一个穿透的完全相同的“十字孔”(阴影部分)，则这个几何体(含内部)的表面积是。
三、作图题(本题满分4分)
-
15. 请用直尺、圆规作图，不写作法，但要保留作图痕迹。
已知：∠α，线段m。
求作：菱形ABCD，使∠A=∠α，对角线AC=m。
四、解答题
-
16. (本题满分8分，每小题4分)(1)、解不等式组 ，并写出它的正整数解；(2)、化简： 。17. 小明和小亮进行“转盘”游戏：下面是两个可以自由转动的转盘，游戏者同时转动两个转盘，如果两个转盘转出的颜色相同，则小明胜；如果转出的颜色可以配成紫色(一个转盘转出红色，另一个转盘转出蓝色)，则小亮胜，这个游戏对两人公平吗？请说明理由。
18. 2020年1月6日，《青岛市生活垃圾分类管理办法》正式施行，这标志着继上海强制实施垃圾分类后，青岛成为山东省首座进入生活垃圾分类法治化城市．某学校团委为了解本校学生对垃圾分类知识的掌握情况，对全校3500名学生进行了一次垃圾分类知识竞赛，并随机抽取了部分试卷进行分析，然后制成了如下不完整的统计图表，请根据图表中信息解答下列问题：组 别
分数分组
人数（频数）
频率
A
50≤x<60
a
0.04
B
60≤x<70
9
0.09
C
70≤x<80
22
0.22
D
80<x<90
b
n
E
90≤x<100
28
0.28
合计
c
1
(注：本次竞赛满分100分，学生得分最低分50分，并且没有满分)
(1)、c= ， n=；(2)、补全频数分布直方图；(3)、该校计划对考试成绩为90<x<100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数。19. 如图，EF表示一座风景秀美的观景山，AC，CE是已经修好的登山步行道。该景区为方便老年游客登顶观景，欲在山脚A与山顶E之间架设一条登山索道AE。在山脚A处测得点C的仰角为24°，在C处测得山顶E的仰角为45°，在山脚A处测得山顶E的仰角为37°．已知步行道AC长640米，则新架设的索道AE长多少米？(参考数据：sin24°≈ ，cos 24°≈ ，tan24°≈ ，sin37°≈ ，cos37°≈ ，tan 37°≈ )
20. 新冠肺炎疫情发生后，社会各界积极行动，以各种方式倾情支援湖北疫区。某车队需要将一批生活物资运送至湖北疫区。已知该车队计划每天运送的货物吨数y(吨)与运输时间x(天)之间满足如图所示的反比例函数关系。
(1)、求该车队计划每天运送的货物吨数y(吨)与运输时间x(天)之间的函数关系式(不需要写出自变量x的取值范围)；(2)、根据计划，要想在5天之内完成该运送任务，则该车队每天至少要运送多少吨物资？(3)、为保证该批生活物资的尽快到位，该车队实际每天运送的货物吨数比原计划多了25%，最终提前了1天完成任务，求实际完成运送任务的天数。21. 如图，矩形EFGH的顶点E，G分别在平行四边形ABCD的边AD，BC上，顶点F，H在平行四边形ABCD的对角线BD上。
(1)、求证：BG=DE；(2)、若E为AD中点，AD=FH，试判断平行四边形ABCD是什么特殊的平行四边形？请说明理由。22. 某商店销售一种商品，经市场调查发现：该商品的日销售量y(件)是售价x(元/件)的一次函数，其售价、日销售量、日销售利润w(元)的三组对应值如下表：售价x(元/件)
50
60
80
日销售量y(件)
100
80
40
日销售利润w(元)
1000
1600
1600
注：日销售利润=日销售量×(售价一进价)
(1)、求日销售量y关于售价x的函数关系式(不要求写出自变量的取值范围)；(2)、由于某种原因，该商品进价提高了5元/件，物价部门规定该商品售价不得超过65元/件，若在今后的销售中，日销售量与售价仍然满足(1)中的函数关系，要使该商店日销售利润最大，则售价应定为多少元？最大利润是多少？23. 【问题提出】如图，有三根针和套在一根针上的n个金属片，按下列规则移动金属片，
规则1：每次只能移动一个金属片；
规则2：较大的金属片不能放在较小的金属片上面．
则把这n个金属片从1号针移到3号针，最少需要移动多少次？
我们从移动1，2，3，4个金属片入手，探究其中的规律性，进而归纳出移动n个金属片所需的次数。
探究一：
当n=1时，只需要把金属片从1号针移到3号针，用符号(13)表示，共移动了1次。(说明：(13)表示把金属片从1号针移到3号针，以此类推)
探究二：
当n=2时，为了避免将较大的金属片放在较小的金属片上面，移动顺序是(本次移动我们借助2号针作为“中间针”)：
(Ⅰ)把第1个金属片从1号针移到2号针；
(Ⅱ)把第2个金属片从1号针移到3号针；
(Ⅲ)把第1个金属片从2号针移到3号针。
用符号表示为：(Ⅰ)(12)；(Ⅱ)(13)；(Ⅲ)(23)，共移动了3次。
探究三：
当n=3时，移动顺序是：
(Ⅰ)把上面两个金属片从1号针移到2号针；
(Ⅱ)把第3个金属片从1号针移到3号针；
(Ⅲ)把上面两个金属片从2号针移到3号针。
(1)、其中(Ⅰ)和(II)都需要借助合适的“中间针”，用符号表示为：(Ⅰ)：(13)(12)(32)；(Ⅱ) (13)；(Ⅲ)；共移动了次。(2)、探究四：当n=4时，移动顺序是：
(Ⅰ)把上面个金属片从1号针移到2号针；
(Ⅱ)把第个金属片从1号针移到3号针；
(Ⅲ)把上面个金属片从2号针移到3号针。
(3)、完成(Ⅰ)需移动次，完成(Ⅲ)需移动次，共移动了次。……
(4)、【问题解决】根据探究一~四，以此类推，你能发现移动规律并对得出的结论进行归纳猜想吗？请你直接写出猜想结果：若把这n个金属片从1号针移到3号针，最少需要移动次。
24. 如图，已知矩形ABCD，AB=6cm，BC=8cm，点P从点D出发，沿DA方向匀速向点A运动，同时，点E从点C出发，沿CA方向匀速向点A运动，速度均为1cm/s；当点P、E中有一点停止运动时，另一点也停止运动，点F为CD中点，连接PE、PF。设运动时间为t(s)(0<t<8)，解答下列问题：
(1)、求当t为何值时，点P运动到∠ABD的平分线上；
(2)、设△PEF的面积为y(cm²) ，求y与t之间的函数关系式；(3)、在运动过程中，是否存在某一时刻t，使得S△PEF：S矩形ABCD=1：8？若存在，求出t的值；若不存在，请说明理由；(4)、连接DE，在运动过程中，是否存在某一时刻t，使得△CDE是等腰三角形。若存在，求出t的值；若不存在，请说明理由。
-