山东省滨州市2019-2020学年七年级下学期数学5月月考试卷
试卷更新日期：2020-07-01 类型：月考试卷
一、选择题：
-
1. 点A(4，-3)在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各式中，正确的是（ ）A、 =±6 B、 = C、 =-4 D、 =-0.63.
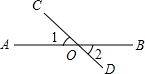
如图，在下列给出的条件中，不能判定AB∥DF的是（ ）
A、∠A+∠2=180° B、∠1=∠A C、∠1=∠4 D、∠A=∠34. 和数轴上的点一一对应的是（ ）A、有理数 B、无理数 C、实数 D、整数和分数5. 下列各数：0.3333…，0，4，-1.5， ， ，-0.525225222中，无理数的个数是（ ）A、0个 B、1个 C、2个 D、3个6. 如图，点A(-2，1)到y轴的距离为（ ）
A、-2 B、1 C、2 D、7. 数轴上两点A，B分别表示实数 和 -1，则两点间的距离是（ ）A、2 B、1 C、2 -1 D、28. 已知 是二元一次方程组 的解，则m－n的值是（ ）A、1 B、2 C、3 D、49. 如图所示的图案可以看作由“基本图案”经过平移得到的是（ ）A、
B、
C、
D、
10. 用加减法解方程组 时，若要求消去 ，则应（ ）A、 B、 C、 D、11. 若一个数的平方根与它的立方根完全相同，则这个数是（ ）A、1 B、-1 C、0 D、±1，012. 在平面直角坐标系中，线段A'B'是由线段AB经过平移得到的，已知点A(-2，1)的对应点为A'(3，-1)，点B的对应点为B'(4，0)，则点B的坐标为（ ）A、(9，-1) B、(-1，0) C、(3，-1) D、(-1，2)二、填空题
-
13. 若 ≈1.414， ≈4.472，则 ≈。14. 如图，直线AB、CD相交于点O ， 若∠1+∠2=100°，则∠BOC等于 ．
15. 已知点M(-4，7)，MN∥x轴，且MN=5，则点N的坐标为。16. 的算术平方根是17. 某正数的平方根是a和a-16，则这个数为。18. 若点A(m+3，1-m)在y轴上，则点A的坐标为。19. 若点P(a，b)在第四象限，则点M(b－a，a－b)在第象限.20. 下列正确说法的是①同位角相等； ②等角的补角相等； ③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直．
三、解答题
-
21.(1)、计算：(2)、用适当的方法解下列方程组①22. 如图，在平面直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为(1，2)。
(1)、填空：点A的坐标是 ， 点B的坐标是。(2)、将△ABC先向左平移2个单位长度， 再向上平移1个单位长度， 得到△A'B'C'，写出△A'B'C'的三个顶点坐标；(3)、求△ABC的面积。23. 阳信县某中学开展以“感受中华传统美德”为主题的研学活动，组织150名学生参观历史博物馆和民俗展览馆，每一名学生只能参加其中一项活动，共支付票款2000元，票价信息如下：地点
票价
历史博物馆
10元/人
民俗展览馆
20元/人
(1)、请问参观历史博物馆和民俗展览馆的人数各是多少人？(2)、若学生都去参观历史博物馆，则能节省票款多少元？24. 如图，CD⊥AB，垂足为D，F是BC上任意一点，FE⊥AB，垂足为E，且∠1=∠2，∠3=80°。
(1)、求证：DG∥BC(2)、求∠BCA的度数。25. 已知5a+2的立方根是3，3a+b-1的算术平方根是4，c是 的整数部分.(1)、求a，b，c的值；(2)、求3a-b+c的平方根.26.(1)、问题发现：如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC。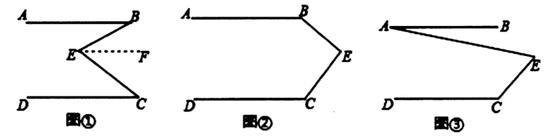
请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC(已知)，EF∥AB(辅助线的作法)．
∴EF∥DC()。
∴∠C=∠CEF（）
∵EF∥AB，∴∠B=∠BEF(同理)。
∴∠B+∠C=。
即∠B+∠C=∠BEC。
(2)、拓展探究：如果点E运动到图②所示的位置，其他条件不变，进一步探究发现：∠B+∠C=360°-∠BEC，请说明理由。(3)、解决问题：如图③，AB∥DC，∠C=120°，∠AEC=80°，请直接写出∠A的度数。