山东省泰安市高新区2019-2020学年七年级下学期数学期中考试试卷（五四学制）

试卷更新日期：2020-07-01 类型：期中考试

进入出卷网下载

一、选择题。

1. 下列事件是随机事件的是（）

A、太阳从东方升起 B、任意画一个三角形内角和是360° C、掷一枚硬币，正面朝上 D、若a为实数，则a²≥0

查看试题解析
2. 二元一次方程组 ${\begin{cases} x - y = 2 \\ 2 x + y = 7 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = - 1 \end{cases}$ C、 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$

查看试题解析
3. 下列命题中，真命题有（）
①垂线段最短；②全等三角形的周长相等；③在同一平面内，平行于同一直线的两条直线平行；④对顶角相等。

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，能判定EB∥AC的是（）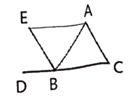

A、∠C=∠ABE B、∠BAC=∠EBD C、∠C=∠ABC D、∠BAC=∠ABE

查看试题解析
5. 已知二元一次方程组 ${\begin{cases} 2 x + 3 y = 12 \\ x + 4 y = 7 \end{cases}$ ，则x-y=（）

A、5 B、4 C、3 D、1

查看试题解析
6. 如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2=44°，则∠1的大小为（）

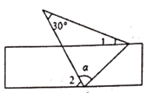A、14° B、16° C、90°-α D、α-44°

查看试题解析
7. 解方程组 ${\begin{cases} 3 x + y = 8 (1) \\ x - y = 1 (2) \end{cases}$ ，下列最佳方法是（）

A、代入法消去x，由(2)得：x=1+y B、代入法消去y，由(1)得：y=1-x=0 C、加减法消去x，由(1)-(2)x3得：4y=5 D、加减法消去y，由(1)+(2)得：4x=9

查看试题解析
8. 对于命题如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（）

A、∠1=50°，∠2=40° B、∠1=50°，∠2=50° C、∠1=40°，∠2=40° D、∠1=45°，∠2=45°

查看试题解析
9. 在70周年国庆阅兵式上，有两辆阅兵车的车牌号分别为：VA01949，VA02019，则数字“9”在这两辆车牌号中出现的概率为（）

A、 $\frac{2}{7}$ B、 $\frac{1}{7}$ C、 $\frac{3}{7}$ D、 $\frac{3}{14}$

查看试题解析
10. 如图，下列条件：①∠1=∠2；②∠4=∠5；③∠2+∠5=180°；④∠1=∠3；⑤∠6+∠4=180°；其中能判断直线l₁∥l₂的有（）

A、②③④ B、②④ C、②④⑤ D、②③⑤

查看试题解析
11. 一次函数y=4x-5与y=kx+b交于点A(1，-1)，则方程组 ${\begin{cases} 4 x - y = 5 \\ k x - y + b = 0 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = - 1 \\ y = 1 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ C、 ${\begin{cases} x = 4 \\ y = 5 \end{cases}$ D、 ${\begin{cases} x = 5 \\ y = 4 \end{cases}$

查看试题解析
12. 某家具厂生产某种配套桌椅(一个桌子两把椅子)，若每块板材生产一张桌子或3把椅子，现计划用这种板材200块生产这批桌椅(不考虑损耗)，设用x块板材生产桌子，y块板材生产椅子，使之正好配套．根据题意所列方程组正确的是（）

A、 ${\begin{cases} x + y = 200 \\ x = 3 y \end{cases}$ B、 ${\begin{cases} x + y = 200 \\ 3 x = y \end{cases}$ C、 ${\begin{cases} x + y = 200 \\ 2 x = 3 y \end{cases}$ D、 ${\begin{cases} x + y = 200 \\ x = 6 y \end{cases}$

查看试题解析

二、填空题

13. 将“三角形的一个外角等于与它不相邻两内角的和”改写成“如果…，那么…”的形式为。

查看试题解析
14. 若|x+y+1|+(3x-2y-2)²=0，则x²-y²=。

查看试题解析
15. 小猫在如图所示的地板上自由地走来走去，它最终停留在阴影方砖上的概率是。

查看试题解析
16. 小明在玩“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题，如图，若AB∥CD，∠BAE=92°，∠DCE=121°，则∠AEC=°。

查看试题解析
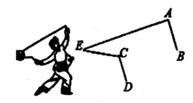17. 若一次函数y=3x-5的图像l₁与y=2x+1的图像l₂相交于点P，则点P的坐标是( ， )。

查看试题解析
18. 如图，在△ABC中，∠B=32°，将△ABC的一部分沿直线m翻折，点B落在点D的位置，则∠1-∠2的度数是°。

查看试题解析

三、解答题

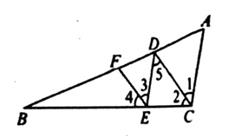
19. 用指定的方法解方程：

(1)、 ${\begin{cases} x + y = 10 \\ y + 2 x = 0 \end{cases}$ (代入消元法)；

(2)、 ${\begin{cases} 2 x + 5 y = 12 \\ 3 x - 2 y = - 1 \end{cases}$ (加减消元法)

查看试题解析
20. 如图，AC∥DE，∠3=∠5，CD平分∠BCA．求证：EF平分∠BED。

查看试题解析
21. 一个不透明的袋子中装有红、黄、白三种颜色的球共10个，这些球除了颜色外完全相同，其中，黄球的个数比白球个数的3倍少2个，从袋中摸出一个球是黄球的概率为0.4。

(1)、分别求袋中红、黄、白三种颜色的球的个数；

(2)、向袋中放入若干个红球，使摸出一个球是红球的概率为0.7，求放入红球的个数；

(3)、在(2)的条件下，求摸出一个球是白球的概率。

查看试题解析
22. 假期期间，小明、小刚各随同家长共15人去某景点游玩，大人票每张100元，学生票8折优惠，买门票时共花费1380元．你能通过计算知道他们几个成人？几个学生吗？

查看试题解析
23. 如图，直线l₁：y=2x-3与x轴交于点D，直线l₂：y=kx+b经过点B(3，1)，且与直线l₁交于点C(m，2)。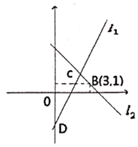

(1)、求点D的坐标：

(2)、求直线l₂的解析式：

(3)、利用函数图象写出关于x，y的二元一次方程组 ${\begin{cases} y = 2 x - 3 \\ y = k x + b \end{cases}$ 的解。

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，AE平分∠BAC，CD是AB边上的高，CD和AE交于点F。判断∠CFE和∠CEF的关系，并说明理由。

查看试题解析
25. 有大小两种盛酒的桶，已知5个大桶和1个小桶共盛酒3斛(古代的一种计量单位)，1个大桶和5个小桶共盛酒2斛。

(1)、求1个大桶和1个小桶各盛酒多少斛；

(2)、若盛酒16斛，需要大小桶几个(写出两种方案即可)

查看试题解析