山西省太原市2019-2020学年八年级下学期数学第二次月考试卷
试卷更新日期：2020-07-01 类型：月考试卷
一、选择题
-
1. 不等式2x-5>3(x-3)的解集为（ ）A、x<-4 B、x>4 C、x<4 D、x>-42. 下列由左边到右边的变形，属于因式分解的是（ ）A、a2-4a+5=(a-2)2+1 B、10x2-5x=5x(2x-1) C、6m3n2=3m3·2n2 D、(x+y)(x-y)=x2-y23. 我国各大银行的Logo设计简洁，寓意深刻，从数学角度看，以下哪个银行Logo是中心
对称图形而不是轴对称图形（ ）
A、
B、
C、
D、
4. 如图，在△ABC中，DE是边AC的垂直平分线，且分别交BC，AC干点D，E，连接AD，若∠B=70°，∠BAD=60°，则∠C为（ ）
A、20° B、25° C、30° D、50°5. 已知一次函数y1=kx+b与y2=ax+c的图象如图所示，则不等式kx+b>ax+c的解集为（ ）
A、x>3 B、x<3 C、x>1 D、x<16. 如图，△ABC沿BC所在直线向左平移4cm得到△A'B'C'，若△ABC的周长为20cm，则四边形A'B'CA的周长为（ ）
A、16cm B、24cm C、28cm D、32cm7. 多项式2a2-18与3a2-18a+27的公因式是（ ）A、a-3 B、a+3 C、a-9 D、a+98. 下列关于直角三角形的命题中是假命题的是（ ）A、一个锐角和斜边分别相等的两个直角三角形全等 B、两直角边分别相等的两个直角三角形全等 C、如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形 D、两个锐角分别相等的两个直角三角形全等9. 用如图1中的三种纸片拼成如图2的矩形，据此可写出一个多项式的因式分解，下列各项正确的是（ ）
A、3a2+3ab+b2=(a+b)(b+3a) B、3a2-3ab+b2=(a-b)(3a+b) C、3a2+4ab+b2=(a+b)(3a+b) D、a2+4ab+3b2=(a+b)(3a+b)10. 如图，将△ABC绕点A按顺时针方向旋转60°后得到△ADE， 连接BD。若AB=8，则图中阴影部分的面积为（ ）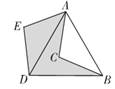
A、16 B、16 C、32 D、32二、填空题
-
11. 用反证法证明“一个三角形中最大的内角不小于60°”时，第一步我们要先假设：。12. 某多项式可以因式分解为a(a+2b)(-2b+a)，则该多项式为。13. 如图，小李想测量学校旗杆的高度，他站在离旗杆(BC)12米的点A处，仰望旗杆顶B，仰角为45°(即∠BDE=45°)。已知小李身高(DA) 为1.5米，则旗杆的高度为米。
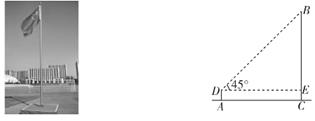14. 某品牌家教机的进价为2000元，标价为2500元，为迎店庆，该商品准备打折出售，但要保持利润率不低于10%，则最多可打几折？若设打x折，可列不等式为：。
15. 如图，大小两圆的圆心都为点O，已知它们的半径分别是R=3.45cm，r=1.45cm，则它们所围成的环形的面积为cm2(结果保留一)。
三、解答题
-
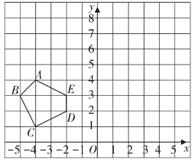
16. 将下列各式因式分解．(1)、x3y2-xy4；(2)、m2n-mn2+ n317. 解不等式组，并写出它的整数解。18. 如图，五边形各顶点的坐标分别为A(-4，4)，B(-5，3)，C(-4，1)，D(-2，2)，E(-2，3)，将五边形先向右平移6个单位长度，再向上平移3个单位长度，得到新五边形A'B'C'D'E'，点A，B，C，D，E分别对应点A'，B'，C'，D'，E'，
(1)、画出平移后的新五边形并标明字母；(2)、如果将新五边形A'B'C'D'E'看成是由原五边形ABCDE经过一次平移得到的，请直接写出这一平移的平移方向和平移距离。19. 利用因式分解证明：365-68能被210整除。20. 如图，已知∠DAC是△ABC的一个外角。
(1)、求作BC边上的高AE及∠DAC的角平分线AF；(尺规作图，不写作法，保留作图痕迹并标明字母)(2)、在(1)的基础上，若AE⊥AF，求证：AB=AC。21. 对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解时，小亮先设a2-4a=b，代入原式后得：
原式=(b+2)(h+6)+4
=b2+8b+16
=(b+4)2
=(a2-4a+4)2
(1)、小亮在因式分解时巧妙运用了以下那种数学思想：__________；A、整体换元思想 B、数形结合思想 C、分类讨论思想(2)、请指出上述因式分解存在的问题并直接写出正确结果；(3)、请参考以上方法对多项式(4a2+4a)(4a2+4a+2)+1进行因式分解。22. 保护环境，人人有责．某小区积极响应政策，为小区安装温馨提示牌和分类垃圾箱，已知购买3个垃圾箱和4个提示牌共需要640元，购买2个垃圾箱和5个提示牌共需要520元。(1)、求垃圾箱与温馨提示牌的单价各是多少？(2)、若该小区计划安放温馨提示牌与垃圾箱共85个，垃圾箱不少于53个、总费用不超过10000元，则共有几种购买方案？(请全部写出)(3)、(2)中哪种方案的花费最少？最少是多少元？
23. 综合与实践材料一：“转化思想”是几何变换中常用的思想，例如将图形进行旋转变换，实现图形位置的“转化”，把一般情形转化为特殊情形，使问题化难为易，它是一种以变化的、运动的观点来处理孤立的、离散问题的思想。
材料二：皮埃尔·德·费马(右图)，17世纪法国律师和业余数学家，被誉为“业余数学家之王”。1638年勒·笛卡儿邀请费马思考关于三个顶点距离为定值的问题，费马经过思考并由此推出费马点的相关结论。
定义：若一个三角形的最大内角小于120°，则在其内部有一点所对三角形三边的张角均为120°，此时该点叫做这个三角形的费马点。如图1，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB=∠BPC=∠CPA=120°，PA+PB+PC的值最小。
(1)、如图2，等边三角形ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数，为了解决本题，小林利用“转化”思想，将△ABP绕顶点A旋转到△ACP'处，连接PP'，此时△ACP'≌△ABP，这样就可以通过旋转变换， 将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=；(2)、如图3，在图1的基础上延长BP，在射线BP上取点D，E，连接AE，AD，使AD=AP，∠DAE=∠PAC，求证：BE=PA+PB+PC；(3)、如图4，在Rt△ABC中，∠ABC=90°，∠ACB=30°，AB=1，点P为Rt△ABC的费马点，连接AP，BP，CP，请直接写出PA+PB+PC的值。