福建省三明市2019-2020学年高三理数(5月份)高考模拟试卷
试卷更新日期:2020-06-30 类型:高考模拟
一、单选题
-
1. 设全集为 , ,则 等于( )A、 B、 C、 D、2. 设 是复数,则下列命题中的假命题是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下图,则下面结论中错误的一个是( )
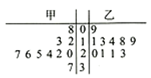 A、甲的极差是29 B、甲的中位数是24 C、甲罚球命中率比乙高 D、乙的众数是214. 定义在R上的函数 为偶函数, , , ,则( )A、 B、 C、 D、5. 设函数 的导函数为 ,则 图象大致是( )A、
A、甲的极差是29 B、甲的中位数是24 C、甲罚球命中率比乙高 D、乙的众数是214. 定义在R上的函数 为偶函数, , , ,则( )A、 B、 C、 D、5. 设函数 的导函数为 ,则 图象大致是( )A、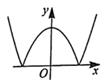 B、
B、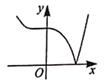 C、
C、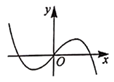 D、
D、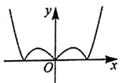 6. 等差数列{an}的前n项和为Sn , 若S17=51,则2a10﹣a11=( )A、2 B、3 C、4 D、67. 执行如图所示的程序框图,若输出的n=6,则输入的整数p的最大值为( )
6. 等差数列{an}的前n项和为Sn , 若S17=51,则2a10﹣a11=( )A、2 B、3 C、4 D、67. 执行如图所示的程序框图,若输出的n=6,则输入的整数p的最大值为( )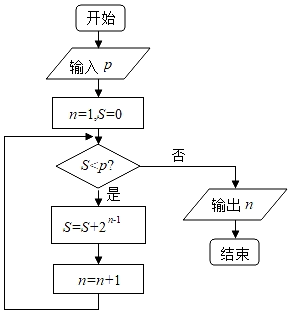 A、7 B、15 C、31 D、638. 关于函数 有下述四个结论:
A、7 B、15 C、31 D、638. 关于函数 有下述四个结论:① 是偶函数;② 在区间 上单调递增;③ 在 上有4个零点;④ 的最大值为2.
其中所有正确结论的编号是( )
A、①②④ B、②④ C、①④ D、①③9. 《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )A、 B、 C、 D、10. 如图,在 中, , 是 上一点,若 ,则实数 的值为( )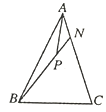 A、 B、 C、 D、11. 直线 经过椭圆 的左焦点F,交椭圆于A、B两点,交y轴于C点,若 ,则该椭圆的离心率是( )A、 B、 C、 D、12. 已知正三棱锥 ,底面是边长为3的正三角形ABC, ,点E是线段AB的中点,过点E作三棱锥 外接球O的截面,则截面面积的最小值是( )
A、 B、 C、 D、11. 直线 经过椭圆 的左焦点F,交椭圆于A、B两点,交y轴于C点,若 ,则该椭圆的离心率是( )A、 B、 C、 D、12. 已知正三棱锥 ,底面是边长为3的正三角形ABC, ,点E是线段AB的中点,过点E作三棱锥 外接球O的截面,则截面面积的最小值是( )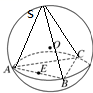 A、3π B、 C、2π D、
A、3π B、 C、2π D、二、填空题
-
13. 已知直线 与曲线 在 处的切线平行,则实数k的值为.14. 若 的展开式中 的系数为-80,则 .15. 若 , 满足约束条件 ,则 的最大值为.16. 对于函数 ,若在定义域内存在实数 满足 ,则称函数 为“倒戈函数”.设 ( 且 )为其定义域上的“倒戈函数”,则实数m的取值范围是 .
三、解答题
-
17. 的周长为 ,且 .(1)、求边 的长;(2)、若 的面积为 ,求角C的度数.18. 某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间 的左侧,则认为该学生属“体能不达标的学生,其中 分别为样本平均数和样本标准差,计算可得 (同一组中的数据用该组区间的中点值作代表).
 (1)、若该校高三某男生的跳远距离为 ,试判断该男生是否属于“体能不达标”的学生?(2)、该校利用分层抽样的方法从样本区间 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在 的概率.19. 如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2, ,
(1)、若该校高三某男生的跳远距离为 ,试判断该男生是否属于“体能不达标”的学生?(2)、该校利用分层抽样的方法从样本区间 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在 的概率.19. 如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2, ,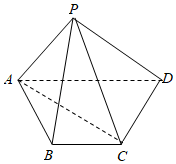
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
20. 已知椭圆N: 经过点 ,且离心率为 .(1)、求椭圆N的标准方程与焦距;(2)、直线l: 与椭圆 的交点为A,B两点,线段 的中点为M.是否存在常数 ,使 恒成立,并说明理由.