福建省龙岩市2019-2020学年高三理数5月教学质量检查试卷

试卷更新日期：2020-06-30 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数z满足 $a_{1} + 2 a_{1} + 4 a_{1} = 7$ ，则z的虚部为（）

A、-1 B、1 C、i D、-i

查看试题解析
2. 已知集合 $A = {x | 0 < x < \sqrt{2}}$ ， $B = {x | \log_{\frac{1}{3}} x < 2}$ ，则 $A \cap B =$ （）

A、 ${x | x > 0}$ B、 ${x | 0 < x < \frac{1}{9}}$ C、 ${x | 0 < x < \sqrt{2}}$ D、 ${x | \frac{1}{9} < x < \sqrt{2}}$

查看试题解析
3. 2020年初，我国突发新冠肺炎疫情，疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示，各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况，现用分层抽样的方法抽取4%小学初中高中学段的学生进行调查，则抽取的样本容量、抽取的高中生家中参与“家务劳动”的人数分别为（）

A、2750，200 B、2750，110 C、1120，110 D、1120，200

查看试题解析
4. 若 $3 \cos 2 α = 2 \sin (\frac{π}{4} - α)$ ， $α \in (\frac{π}{2} ， π)$ 则 $\sin 2 α$ 的值为（）

A、 $- \frac{4 \sqrt{2}}{9}$ B、 $- \frac{5 \sqrt{2}}{9}$ C、 $- \frac{7}{9}$ D、 $\frac{7}{9}$

查看试题解析
5. 某三棱锥的三视图如图所示，如果网格纸上小正方形的边长为1，则该三棱锥的体积为（）

A、4 B、8 C、12 D、24

查看试题解析
6. 已知A，B，C三点不共线，若 $\vec{B C} = 3 \vec{C D}$ 点E为线段AD的中点，且 $\vec{A E} = x \vec{A B} + y \vec{A C}$ ，则 $x + y$ 的值为（）

A、 $- \frac{1}{6}$ B、 $\frac{1}{2}$ C、1 D、 $\frac{3}{2}$

查看试题解析
7. 已知函数 $f (x) = (| \sin x | + \sin x) \cdot \cos x$ ，则下列命题中正确的是（）

A、 $f (x)$ 的最小正周期为π B、 $f (x)$ 的图象关于直线 $x = \frac{π}{4}$ 对称 C、 $f (x)$ 的值域为 $[0 ， 1]$ D、 $f (x)$ 在区间 $[\frac{π}{4} ， \frac{3 π}{4}]$ 上单调递减

查看试题解析
8. 分形几何是一门以不规则几何形态为研究对象的几何学，科赫曲线是比较典型的分形图形，1904年瑞典数学家科赫第一次描述了这种曲线，因此将这种曲线称为科赫曲线.其生成方法是：（I）将正三角形（图（1））的每边三等分，以每边三等分后的中间的那一条线段为一边，向形外作等边三角形，并将这“中间一段”去掉，得到图（2）；（II）将图（2）的每边三等分，重复上述的作图方法，得到图（3）；（Ⅲ）再按上述方法继续做下去……，设图（1）中的等边三角形的边长为1，并且分别将图（1）、图（2）、图（3）、…、图（n）、…中的图形依次记作 $M_{1}$ ， $M_{2}$ ， $M_{3}$ ，…， $M_{n}$ ，…，设 $M_{n}$ 的周长为 $L_{n}$ ，则 $L_{4}$ 为（）

A、 $\frac{32}{9}$ B、 $\frac{16}{3}$ C、 $\frac{64}{9}$ D、 $\frac{256}{27}$

查看试题解析
9. 已知函数 $f (x) = \frac{e^{x} - 1}{e^{x} + 1} \cos (3 x + α) ， α \in [0 ， π]$ ，则 $f (x)$ 的图象不可能是（）

A、 B、 C、 D、

查看试题解析
10. 设双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， $| F_{1} F_{2} | = 2 c$ ，过 $F_{2}$ 作x轴的垂线，与双曲线在第一象限的交点为A，点Q坐标为 $(c ， \frac{3 a}{2})$ 且满足 $| F_{2} Q | > | F_{2} A |$ ，若在双曲线C的支上存在点P使得 $| P F_{1} | + | P Q | < \frac{7}{6} | F_{1} F_{2} |$ 成立，则双曲线C的离心率的取值范围是（）

A、 $(1 ， \frac{\sqrt{10}}{2})$ B、 $(1 ， \frac{3}{2})$ C、 $(\frac{3}{2} ， \frac{\sqrt{10}}{2})$ D、 $(\frac{3}{2} ， + \infty)$

查看试题解析
11. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，P是正方形 $A D D_{1} A_{1}$ 内（包括边界）的动点，M是CD的中点，且 $∠ P B A = ∠ P M D$ ，则当 $△ P A D$ 的面积最大时， $| P A |$ 的值为（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{4 \sqrt{2}}{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
12. 已知各项都为正数的数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{n + 1} = \ln a_{n} + \frac{1}{a_{n}^{2}} + \frac{3}{2}$ ， $b_{n} = [a_{n}]$ ，其中 $[a_{n}]$ 表示不超过 $a_{n}$ 的最大整数，则 $b_{5}$ 的值为（）
（参考数据： $\ln 2 \approx 0.69$ ， $\ln 3 \approx 1.10$ ， $\ln 5 = 1.61$ ）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 在 ${(x - \frac{1}{2 x})}^{6} (x + 3)$ 的展开式中，常数项为.

查看试题解析
14. 已知抛物线 $E : y^{2} = 8 x$ 的焦点为F，过抛物线E上一点P（在第一象限内）作y轴的垂线PQ，垂足为Q，若四边形OFPQ的周长为7，则点P的坐标为.

查看试题解析
15. 实现国家富强.民族复兴.人民幸福是“中国梦”的本质内涵.某商家计划以“全民健身促健康，同心共筑中国梦”为主题举办一次有奖消费活动，此商家先把某品牌乒乓球重新包装，包装时在每个乒乓球上印上“中”“国”“梦”三个字样中的一个，之后随机装盒（1盒4个球），并规定：若顾客购买的一盒球印的是同一个字，则此顾客获得一等奖；若顾客购买的一盒球集齐了“中”“国”二字且仅有此二字，则此顾客获得二等奖；若顾客购买的一盒球集齐了“中”“国”“梦”三个字，则此顾客获得三等奖，其它情况不设奖，则顾客购买一盒乒乓球获奖的概率是.

查看试题解析
16. 如图，在平面直角坐标系xOy中，边长为2的正方形ABCD沿x轴滚动（无滑动滚动），点D恰好经过坐标原点，设顶点 $B (x ， y)$ 的轨迹方程是 $y = f (x)$ ，则 $f (19) =$ .

查看试题解析

三、解答题

17. 在锐角 $△ A B C$ 中，内角A，B，C的对边分别为a，b，c，已知 $2 b - c = \frac{2 a b c \cos C}{b^{2} + c^{2} - a^{2}}$ .

(1)、求A的值；

(2)、若 $c = 2$ ，求 $△ A B C$ 面积的取值范围.

查看试题解析
18. 在四棱锥P-ABCD中，底面ABCD为直角梯形， $∠ A D C = ∠ B C D = 90 °$ ， $B C = 1$ ， $P D = A D = 2 D C = 2$ ， $∠ P D A = 60 °$ ，且平面 $P A D ⊥$ 平面ABCD．

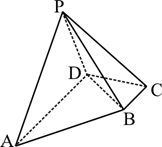(1)、求证： $B D ⊥ P C$ ；

(2)、在线段PA上是否存在一点M，使二面角M-BC-D的大小为 $30 °$ ？若存在，求出 $\frac{P M}{P A}$ 的值；若不存在，请说明理由.

查看试题解析
19. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，M为椭圆上任意一点，当 $∠ F_{1} M F_{2} = 60^{\circ}$ 时， $△ F_{1} M F_{2}$ 的面积为 $\sqrt{3}$ ，且 $2 b = \sqrt{3} a$ .

(1)、求椭圆C的方程；

(2)、已知直线 $l$ 经点 $N (2, 3)$ ，与椭圆C交于不同的两点P、Q，且 $\vec{N P} \cdot \vec{N Q} = \frac{48}{5}$ ，求直线l的方程.

查看试题解析

20. 交强险是车主必须为机动车购买的险种，实行的是费率浮动机制，保费与上一年度车辆发生道路交通事故的情况相联系.每年交强险最终保险费计算方法是：交强险最终保险费

= a \cdot (1 + A)

，其中a为交强险基础保险费，A为与道路交通事故相联系的浮动比率，同时满足多个浮动因素的，按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定：普通6座以下私家车的交强险基础保险费a为950元，交强险费率浮动因素及比率如下表：

交强险浮动因素和浮动费率比率表
类型	浮动因素	浮动比率
$A_{1}$	上一个年度未发生有责任道路交通事故	-10%
$A_{2}$	上两个年度未发生有责任道路交通事故	-20%
$A_{3}$	上三个及以上年度未发生有责任道路交通事故	-30%
$A_{4}$	上一个年度发生一次有责任不涉及死亡的道路交通事故	0%
$A_{5}$	上一个年度发生两次及以上有责任道路交通事故	10%
$A_{6}$	上一个年度发生有责任道路交通死亡事故	30%

某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况，统计结果如下表：

类型	$A_{1}$	$A_{2}$	$A_{3}$	$A_{4}$	$A_{5}$	$A_{6}$
数量	25	10	10	25	20	10

以这100辆该品牌车的投保类型的频率代替一辆车投保类型的概率，完成下列问题.

(1)、记X为一辆该品牌车在第四年续保时的费用，求X的分布列与数学期望（数学期望值保留到个位数字）；

(2)、某二手车销售商专门销售这一品牌的二手车，且将经销商购车后下一年的交强险最终保险费高于交强险基础保险费a的车辆记为事故车，假设购进一辆事故车亏损3000元，购进一辆非事故车盈利5000元.

①若该销售商购进三辆（车龄已满三年）该品牌二手车，求这三辆车中至少有一辆是事故车的概率；

②若该销售商一次购进100辆（车龄已满三年）该品牌二手车，求他获得利润的期望.

查看试题解析

21. 已知 $f (x) = {(\ln x)}^{^{2}} + 2 x - a e^{x}$ .

(1)、证明 $f (x)$ 在 $x = 1$ 处的切线恒过定点；

(2)、若 $f (x)$ 有两个极值点，求实数a的取值范围.

查看试题解析
22. 在直角坐标系xOy中，直线l过点 $(- 2, 0)$ 且倾斜角为 $α$ .以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为 $ρ = 1$ ，l与C交于M，N两点.

(1)、求C的直角坐标方程和 $α$ 的取值范围；

(2)、求MN中点H的轨迹的参数方程.

查看试题解析
23. 已知函数 $f (x) = | x + 1 | - 2 | x - m | (m > 0)$ ，且 $f (x)$ 的最大值为3.

(1)、求m的值；

(2)、若正数a，b，c满足 $2 (a + b + c) = m$ ，证明： $b c (1 - a) + a c (1 - b) + a b (1 - c) \geq 6 a b c$ .

查看试题解析