辽宁省辽南协作校2020届高三理数第一次模拟考试试卷

试卷更新日期：2020-06-30 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {0 ， x^{2}}$ ， $N = {1 ， 2}$ ，若 $M \cap N = {2}$ ，则 $M \cup N =$ （）

A、 ${0 ， x^{2} ， 1 ， 2}$ B、 ${2 ， 0 ， 1 ， 2}$ C、 ${0 ， 1 ， 2}$ D、 ${0 ， 1 ， - \sqrt{2} ， \sqrt{2} ， 2}$

查看试题解析
2. 已知复数z满足 $(1 + i) z = | 2 i |$ ，i为虚数单位，则z等于（）

A、 $1 - i$ B、 $1 + i$ C、 $\frac{1}{2} - \frac{1}{2} i$ D、 $\frac{1}{2} + \frac{1}{2} i$

查看试题解析
3. 设 $\vec{a}, \vec{b}$ 是向量，则“ $| \vec{a} | = | \vec{b} |$ ”是“ $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 若空间中三条两两不同的直线 $l_{1}$ ， $l_{2}$ ， $l_{3}$ ，满足 $l_{1} ⊥ l_{2}$ ， $l_{2} ⊥ l_{3}$ ，则下列结论一定正确的是（）

A、 $l_{1} ⊥ l_{3}$ B、 $l_{1}$ 与 $l_{3}$ 既不垂直又不平行 C、 $l_{1} / /$ $l_{3}$ D、 $l_{1}$ 与 $l_{3}$ 的位置关系不确定

查看试题解析
5. 已知正三棱锥 $P - A B C$ ，点P、A、B、C都在直径为 $\sqrt{3}$ 的球面上，若 $P A$ 、 $P B$ 、 $P C$ 两两互相垂直，则该正三棱锥的体积为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{12}$

查看试题解析
6. 点 $M (5, 3)$ 到抛物线 $y = a x^{2}$ 的准线的距离为6，则该抛物线的方程是（）

A、 $y = 12 x^{2}$ B、 $y = - 36 x^{2}$ C、 $y = 12 x^{2}$ 或 $y = - 36 x^{2}$ D、 $y = \frac{1}{12} x^{2}$ 或 $y = - \frac{1}{36} x^{2}$

查看试题解析
7. 函数 $y = {cos}^{2} x + sin x - 1$ 的值域为（）

A、 $(- \infty, \frac{1}{4}]$ B、 $[0, \frac{1}{4}]$ C、 $[- 2, \frac{1}{4}]$ D、 $[- 2, 0]$

查看试题解析
8. 函数 $f (x) = \frac{e^{x} + 1}{| x | (e^{x} - 1)}$ 的图像大致为（）

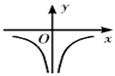A、 B、 C、 D、

查看试题解析
9. 函数 $f (x) = A sin (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，为了得到 $y = sin 2 x$ 的图象，只需将 $f (x)$ 的图象 $($ $)$

A、向右平移 $\frac{π}{3}$ 个单位 B、向右平移 $\frac{π}{6}$ 个单位 C、向左平移 $\frac{π}{3}$ 个单位 D、向左平移 $\frac{π}{6}$ 个单位

查看试题解析
10. 如图所示，为了测量A，B处岛屿的距离，小明在D处观测，A，B分别在D处的北偏西15°、北偏东45°方向，再往正东方向行驶40海里至C处，观测B在C处的正北方向，A在C处的北偏西60°方向，则A，B两处岛屿间的距离为（）

A、 $20 \sqrt{6}$ 海里 B、 $40 \sqrt{6}$ 海里 C、 $20 (1 + \sqrt{3})$ 海里 D、40海里

查看试题解析
11. 甲、乙两位同学各拿出六张游戏牌，用作投骰子的奖品，两人商定：骰子朝上的面的点数为奇数时甲得1分，否则乙得1分，先积得3分者获胜得所有12张游戏牌，并结束游戏．比赛开始后，甲积2分，乙积1分，这时因意外事件中断游戏，以后他们不想再继续这场游戏，下面对这12张游戏牌的分配合理的是（　　）

A、甲得9张，乙得3张 B、甲得6张，乙得6张 C、甲得8张，乙得4张 D、甲得10张，乙得2张

查看试题解析
12. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两顶点分别为 $A_{1}$ ， $A_{2}$ ，F为双曲线的一个焦点，B为虚轴的一个端点，若在线段 $B F$ （不含端点）上存在两点 $P_{1}$ ， $P_{2}$ ，使得 $∠ A_{1} P_{1} A_{2} = ∠ A_{1} P_{2} A_{2} = \frac{π}{2}$ ，则双曲线的渐近线斜率的平方的取值范围是（）

A、 $(1 ， \frac{\sqrt{5} + 1}{2})$ B、 $(1 ， \frac{\sqrt{3} + 1}{2})$ C、 $(0 ， \frac{\sqrt{5} + 1}{2})$ D、 $(\frac{\sqrt{3} + 1}{2} ， \frac{3}{2})$

查看试题解析

二、填空题

13. 已知函数 $f (x) = {\begin{array}{l} \log_{9} (x^{2} - 1), x > 0 \\ 2^{x + 1}, x \leq 0 \end{array}$ ，则 $f (\sqrt{10}) + f (0) =$ ．

查看试题解析
14. 我国古代数学名著《数术九章）有“米谷粒分”题：粮仓开仓收粮，有人送来米1530石，验得米内夹谷，抽样取米一把，数得252粒内夹谷28粒.估计这批米内所夹的谷有石.

查看试题解析
15. 考古学家经常利用碳14的含量来推断古生物死亡的大致时间.当有机体生存时，会持续不断地吸收碳14，从而其体内的碳14含量会保持在一定的水平；但当有机体死亡后，就会停止吸收碳14，其体内的碳14含量就会逐渐减少，而且每经过大约5730年后会变为原来的一半.假设有机体生存时碳14的含量为1，如果用y表示该有机体死亡x年后体内碳14的含量，则y与x的关系式可以表示为.

查看试题解析
16. 已知 $f (x) = x (e + \ln x)$ ， $g (x) = \frac{1}{3} x^{3} + \frac{3}{2} x + m$ ，对于 $\forall x \in [\frac{1}{2} ， + \infty)$ 时都有 $f (x) \leq g (x)$ 恒成立，则m的取值范围为.

查看试题解析

三、解答题

17. 数列 ${a_{n}}$ 的前n项和 $S_{n}$ ，满足 $S_{n} = \frac{3}{2} a_{n} - \frac{1}{2} a_{1}$ ，且 $a_{1} = 3$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{2 \log_{3} a_{n} - 1}{a_{n}}$ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ .

查看试题解析
18. 港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地，大大缩短了三地的时空距离，盘活了珠江三角洲的经济，被誉为新的世界七大奇迹.截至2019年10月23日8点，珠海公路口岸共验放出入境旅客超过1400万人次，日均客流量已经达到4万人次，验放出入境车辆超过70万辆次，2019年春节期间，客流再次大幅增长，日均客流达8万人次，单日客流量更是创下11.3万人次的最高纪录.
2019年从五月一日开始的连续100天客流量频率分布直方图如下

(1)、①同一组数据用该区间的中点值代替，根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.

(2)、设这100天中客流量超过5万人次的有 $n$ 天，从这 $n$ 天中任取两天，设 $X$ 为这两天中客流量超过7万人的天数.求 $X$ 的分布列和期望．

查看试题解析
19. 如图，四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} ⊥$ 平面 $A B C D$ ， $A B // D C$ ， $A B ⊥ A D$ ， $A D = C D = 1$ ， $A A_{1} = A B = 2$ ，E为棱 $A A_{1}$ 的中点

(1)、证明： $B_{1} C_{1} ⊥ C E$ ；

(2)、设点M在线段 $C_{1} E$ 上，且直线 $A M$ 与平面 $A D D_{1} A_{1}$ 所成角的正弦值为 $\frac{\sqrt{2}}{6}$ ，求线段 $A M$ 的长.

查看试题解析
20. 已知椭圆 $C$ 的标准方程是 $\frac{x^{2}}{6} + \frac{y^{2}}{2} = 1$ ，设F是椭圆C的左焦点，T为直线 $x = - 3$ 上任意一点，过F做 $T F$ 的垂线交椭圆C于点P，Q.

(1)、证明：线段 $O T$ 平分线段 $P Q$ （其中O为坐标原点）；

(2)、当 $\frac{| T F |}{| P Q |}$ 最小时，求点T的坐标.

查看试题解析
21. 已知函数 $f (x) = \cos x + x \sin x + e^{x} - a x$

(1)、若函数 $f (x)$ 在点 $(0 ， f (0))$ 处的切线与x轴平行，求实数a的值及函数 $f (x)$ 在区间 $[- \frac{π}{2} ， \frac{π}{2}]$ 上的单调区间；

(2)、在（1）的条件下，若 $x_{1} \neq x_{2}$ ， $f (x_{1}) = f (x_{2})$ ，求证： $f^{'} (\frac{x_{1} + x_{2}}{2}) < 0$ .（ $f^{'} (x)$ 为 $f (x)$ 的导函数）

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = 3 + t \cos α \\ y = t \sin α \end{array}$ （t为参数， $0 \leq α < π$ ），在极坐标系（与平面直角坐标系取相同的单位长度，以坐标原点O为极点， $x$ 轴正半轴为极轴）中，曲线 $C_{2}$ 的极坐标方程为 $ρ + 2 \cos θ = 0$ .

(1)、若 $α = \frac{π}{4}$ 可，试判断曲线 $C_{1}$ 和 $C_{2}$ 的位置关系；

(2)、若曲线 $C_{1}$ 与 $C_{2}$ 交于点M，N两点，且 $P (3, 0)$ ，满足 $| P M | + | P N | = 5 | M N |$ .求 $\sin α$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 2 x + 4 |$ .
（Ⅰ）解不等式： $f (x) \geq - 3 x + 4$ ；

（Ⅱ）若函数 $f (x)$ 的最小值为 $a$ ，且 $m + n = a (m > 0, n > 0)$ ，求 $\frac{1}{m} + \frac{1}{n}$ 的最小值.

查看试题解析