江苏省苏州市吴江区2020届高三下学期数学五月统考试卷

试卷更新日期：2020-06-30 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知集合 $A = {1, 2, 3, 4}$ ，集合 $B = {4, 5}$ ，则 $A \cap B =$ .

查看试题解析
2. 复数 $z = i (1 + 4 i)$ ，(其中i为虚数单位)的实部为．

查看试题解析
3. 函数f（x）=lnx+ $\sqrt{1 - x}$ 的定义域为．

查看试题解析
4. 已知某地连续5天的最低气温（单位：摄氏度）依次是18，21，22，24，25，那么这组数据的方差为.

查看试题解析
5. 我国古代数学名著《九章算术》有一抽样问题：“今有北乡若干人，西乡七千四百八十八人，南乡六千九百一十二人，凡三乡，发役三百人，而北乡需遣一百零八人，问北乡人数几何？”其意思为：“今有某地北面若干人，西面有7488人，南面有6912人，这三面要征调300人，而北面征调108人（用分层抽样的方法），则北面共有人．”

查看试题解析
6. 已知椭圆 $\frac{x^{2}}{10 - m} + \frac{y^{2}}{m - 2} = 1$ 的长轴在 $y$ 轴上，若焦距为4，则 $m =$ .

查看试题解析
7. 如图是一个算法的程序框图，当输入的值x为8时，则其输出的结果是．

查看试题解析
8. 已知角 $α$ 的顶点与坐标原点重合，始边与x轴的正半轴重合，终边经过点 $P (- 1, 2)$ ，则 $s i n 2 α =$ ．

查看试题解析
9. 已知函数 $f (x) = \log_{a} (\sqrt{x^{2} + a} - x) + b$ ，若 $f (3) - f (- 3) = - 1$ ，则实数a的值是．

查看试题解析
10. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，E为棱 $D D_{1}$ 上的点， $F$ 为AB的中点，则三棱锥 $B_{1} - B F E$ 的体积为.

查看试题解析
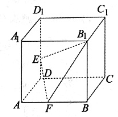11. 已知x ， y为正数，且 $\frac{1}{2 + x} + \frac{4}{y} = 1$ ，则 $x + y$ 的最小值为.

查看试题解析
12. 如图所示，平行四边形 $A B C D$ 中， $A B = 2 A D = 2$ ， $∠ B A D = 60 °$ ， $E$ 是 $D C$ 中点，那么向量 $\overset{⇀}{A C}$ 与 $\overset{⇀}{E B}$ 所成角的余弦值等于.

查看试题解析
13. 设△ABC的三边a ， b ， c ，所对的角分别为A ， B ， C ．若 $b^{2} + 3 a^{2} = c^{2}$ ，则 $\tan A$ 的最大值是．

查看试题解析
14. 任意实数a ， b ，定义 $a \otimes b = {\begin{array}{l} a b a b \geq 0 \\ \frac{a}{b} a b < 0 \end{array}$ ，设函数 $f (x) = \ln x \otimes x$ ，正项数列 ${a_{n}}$ 是公比大于0的等比数列，且 $a_{1010} = 1, f (a_{1}) + f (a_{2}) + f (a_{3}) + \dots + f (a_{2019}) + f (a_{2020}) = - e$ ，则 $a_{2020}$ = ．

查看试题解析

二、解答题

15. $△ A B C$ 中的内角A，B，C的对边分别为a，b，c，已知 $a = 2$ ， $B = - \frac{π}{3}$ ， $\vec{A B} \cdot \vec{A C} = 6$ ．

(1)、求边 $c$ 的值；

(2)、求 $\sin (A - C)$ 的值．

查看试题解析
16. 在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A C$ ， $B B_{1} = B C$ ，点P，Q，R分别是棱 $B C$ ， $C C_{1}$ ， $B_{1} C_{1}$ 的中点．

(1)、求证： $A_{1} R / /$ 平面 $A P Q$ ；

(2)、求证：直线 $B_{1} C ⊥$ 平面 $A P Q$ ．

查看试题解析
17. 如图，为方便市民游览市民中心附近的“网红桥”，现准备在河岸一侧建造一个观景台P，已知射线 $A B$ ， $A C$ 为两边夹角为 $120 °$ 的公路（长度均超过 $\sqrt{3}$ 千米），在两条公路 $A B$ ， $A C$ 上分别设立游客上下点M，N，从观景台P到M，N建造两条观光线路 $P M$ ， $P N$ ，测得 $A M = \sqrt{3}$ 千米， $A N = \sqrt{3}$ 千米．

(1)、求线段 $M N$ 的长度；

(2)、若 $∠ M P N = 60 °$ ，求两条观光线路 $P M$ 与 $P N$ 之和的最大值．

查看试题解析
18. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，点 $N (2 ， 0)$ 椭圆的右顶点.

(1)、求椭圆的方程；

(2)、过点 $H (0 ， 2)$ 的直线 $l$ 与椭圆交于 $A ， B$ 两点，直线 $N A$ 与直线 $N B$ 的斜率和为 $- \frac{1}{3}$ ，求直线l的方程.

查看试题解析
19. 已知函数 $f (x) = e^{x} + x^{2} - x$ ， $g (x) = x^{2} + a x + b$ ， $a ， b \in R$ ．

(1)、当 $a = 1$ 时，求函数 $F (x) = f (x) - g (x)$ 的单调区间；

(2)、若曲线 $y = f (x) - g (x)$ 在点(1，0)处的切线为l ： x＋y－1＝0，求a ， b的值；

(3)、若 $f (x) \geq g (x)$ 恒成立，求a+b的最大值．

查看试题解析
20. 记无穷数列 ${a_{n}}$ 的前n项 $a_{1}$ ， $a_{2}$ ，…， $a_{n}$ 的最大项为 $A_{n}$ ，第n项之后的各项 $a_{n + 1}$ ， $a_{n + 2}$ ，…的最小项为 $B_{n}$ ， $b_{n} = A_{n} - B_{n}$ ．

(1)、若数列 ${a_{n}}$ 的通项公式为 $a_{n} = 2 n^{2} - 7 n + 6$ ，写出 $b_{1}$ ， $b_{2}$ ， $b_{3}$ ；

(2)、若数列 ${b_{n}}$ 的通项公式为 $b_{n} = 1 - 2 n$ ，判断 ${a_{n + 1} - a_{n}}$ 是否为等差数列，若是，求出公差；若不是，请说明理由；

(3)、若数列 ${b_{n}}$ 为公差大于零的等差数列，求证： ${a_{n + 1} - a_{n}}$ 是等差数列．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，直线 $x + y - 2 = 0$ 在矩阵 $A = [\begin{array}{l} 1 & a \\ b & 2 \end{array}]$ 对应的变换作用下得到的直线仍为 $x + y - 2 = 0$ ，求矩阵A.

查看试题解析
22. 在极坐标系中，直线 $l$ 的极坐标方程为 $θ = \frac{π}{3} (ρ \in R)$ ．以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C的参数方程为 ${\begin{array}{l} x = 2 \sin α \\ y = 1 - \cos 2 α \end{array}$ （ $α$ 为参数）．求直线l与曲线C交点P的直角坐标．

查看试题解析
23. 已知x，y，z均为正数，且 $\frac{1}{x + 1} + \frac{1}{y + 1} + \frac{1}{z + 1} \leq \frac{3}{2}$ ，求证： $x + 4 y + 9 z \geq 10$ ．

查看试题解析
24. 如图，在三棱锥 $D - A B C$ 中， $D A ⊥$ 平面 $A B C$ ， $∠ C A B = 90 °$ ，且 $A C = A D = 1$ ， $A B = 2$ ，E为 $B D$ 的中点．

(1)、求异面直线 $A E$ 与 $B C$ 所成角的余弦值；

(2)、求二面角 $A - C E - B$ 的余弦值．

查看试题解析
25. 在自然数列 $1, 2, 3, \dots, n$ 中，任取 $k$ 个元素位置保持不动，将其余 $n - k$ 个元素变动位置，得到不同的新数列.由此产生的不同新数列的个数记为 $P_{n} (k)$ .

(1)、求 $P_{3} (1)$ ；

(2)、求 $\sum_{k = 0}^{4} P_{4} (k)$ ；

(3)、证明 $\sum_{k = 0}^{n} k P_{n} (k) = n \sum_{k = 0}^{n - 1} P_{n - 1} (k)$ ，并求出 $\sum_{k = 0}^{n} k P_{n} (k)$ 的值.

查看试题解析