浙江省嘉兴市、舟山市2020年中考数学试卷
试卷更新日期:2020-06-28 类型:中考真卷
一、选择题(本题有10小题,每题3分,共30分)
-
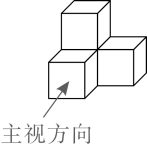
1. 2020年3月9日,中国第54颗北斗导航卫星成功发射,其轨道高度约为36000000m。数36000000用科学记数法表示为( )A、 0.36×108 B、36×107 C、3.6×108 D、3.6×1072. 下图是由四个相同的小正方体组成的立体图形,它的主视图为( )
 A、
A、 B、
B、 C、
C、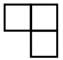 D、
D、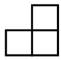 3. 已知样本数据2,3,5,3,7,下列说法不正确的是( )A、平均数是4 B、众数是3 C、中位数是5 D、方差是3.24. 一次函数y=2x-1的图象大致是( )A、
3. 已知样本数据2,3,5,3,7,下列说法不正确的是( )A、平均数是4 B、众数是3 C、中位数是5 D、方差是3.24. 一次函数y=2x-1的图象大致是( )A、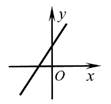 B、
B、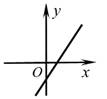 C、
C、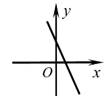 D、
D、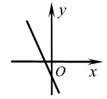 5. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0)。以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标为( )
5. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0)。以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标为( )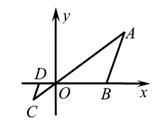 A、(-1,-1). B、( , -1) C、(-1, ) D、(-2,-1).6. 不等式3(1-x)>2-4x的解在数轴上表示正确的是( )A、
A、(-1,-1). B、( , -1) C、(-1, ) D、(-2,-1).6. 不等式3(1-x)>2-4x的解在数轴上表示正确的是( )A、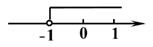 B、
B、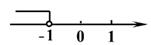 C、
C、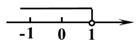 D、
D、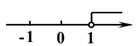 7. 如图,正三角形ABC的边长为3, 将△ABC绕它的外心O逆时针旋转60°得到△A'B'C',则它们重叠部分的面积是( )
7. 如图,正三角形ABC的边长为3, 将△ABC绕它的外心O逆时针旋转60°得到△A'B'C',则它们重叠部分的面积是( )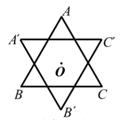 A、2 B、 C、 D、8. 用加减消元法解二元一次方程组: 时,下列方法中无法消元的是( )A、①×2-② B、②×(-3)-① C、①×(-2)+②. D、①-②×39. 如图,在等腰△ABC中, AB=AC=2 ,BC=8, 按下列步骤作图:
A、2 B、 C、 D、8. 用加减消元法解二元一次方程组: 时,下列方法中无法消元的是( )A、①×2-② B、②×(-3)-① C、①×(-2)+②. D、①-②×39. 如图,在等腰△ABC中, AB=AC=2 ,BC=8, 按下列步骤作图:
①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于 EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于 AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点0;③以点为圆心,线段OA长为半径作圆。则⊙O的半径为( )
A、2 B、10 C、4 D、510. 已知二次函数y=x²,当a≤x≤b时m≤y≤n,则下列说法正确的是( )A、当n-m=1时,b-a有最小值 B、当n-m=1时,b-a有最大值 C、当b-a=1时,n-m无最小值 D、当b-a=1时,n-m有最大值二、填空题(本题有6小题,每题4分,共24分)
-
11. 分解因式:x²-9=。12. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。
 13. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是 。
13. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是 。 14. 如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。
14. 如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。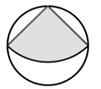 15. 数学家斐波那契编写的《算经》中有如下问题:一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第一次分钱的人数,设第一次分钱的人数为x人,则可列方程。16. 如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm。现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上。当点B'恰好落在边CD上时,线段BM的长为cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为cm。
15. 数学家斐波那契编写的《算经》中有如下问题:一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第一次分钱的人数,设第一次分钱的人数为x人,则可列方程。16. 如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm。现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上。当点B'恰好落在边CD上时,线段BM的长为cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为cm。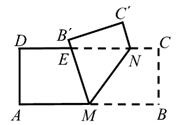
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、计算:(2020)0- +|-3|;(2)、化简:(a+2)(a-2)-a(a+1).18. 比较x2+1与2x的大小。(1)、尝试(用“<”,“=”或“>”填空):
①当x=1时,x²+12x;
②当x=0时,x2+12x;
③当x=-2时,x2+12x。
(2)、归纳:若x取任意实数,x2+1与2x有怎样的大小关系?试说明理由.19. 已知:如图,在△OAB中,OA=OB,⊙O与AB相切于点C。求证:AC=BC。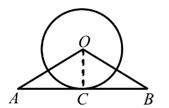
小明同学的证明过程如下框:
证明:连结OC
∵OA=OB,∴∠A=∠B
又∵OC=OC,
∴△OAC≌OBC,
∴AC=BC
小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程。
20. 经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表。x
1
2
3
4
5
6
y
6
2.9
2
1.5
1.2
1
 (1)、请画出相应函数的图象,并求出函数表达式。(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上。若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由。21. 小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
(1)、请画出相应函数的图象,并求出函数表达式。(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上。若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由。21. 小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
根据上述三个统计图,请解答:
(1)、2014~2019年三种品牌电视机销售总量最多的是品牌,月平均销售量最稳定的是品牌。(2)、2019年其他品牌的电视机年销售总量是多少万台?(3)、货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由。22. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向。测量方案与数据如下表: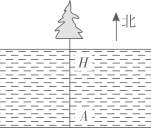
课题
测量河流宽度
测量工具
测量角度的仪器,皮尺等
测量小组
第一小组
第二小组
第三小组
测量方案示意图
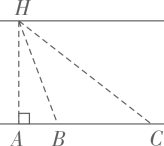
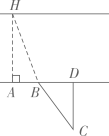

说明
点B,C在点A的正东方向
点B,D在点A的正东方向
点B在点A的正东方向,点C在点A的正西方向
测量数据
BC=60m,
∠ABH=70°,
∠ACH=35°
BD=20m,
∠ABH=70°,
∠BCD=35°
BC=101m,
∠ABH=70°,
∠ACH=35°
(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)
(1)、哪个小组的数据无法计算出河宽?(2)、请选择其中一个方案及其数据求出河宽(精确到0.1m)。23. 在一次数学研究性学习中, 小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1) ,其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动。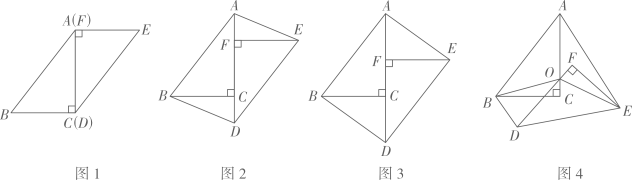 (1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。
(1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。【思考】图2中的四边形ABDE是平行四边形吗?请说明理由。
【发现】当纸片DEF平移到某一位置时,小兵发现四边形AB DE为矩形(如图3)。求AF的长。
(2)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4)。【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由。
24. 在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B。 (1)、求该抛物线的函数表达式。(2)、当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m。
(1)、求该抛物线的函数表达式。(2)、当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m。①求OD的长。
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3)。东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=-2(t-0.5)²+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同)。东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计)。