广西梧州市2018-2019学年高二下学期理数期末考试试卷
试卷更新日期:2020-06-28 类型:期末考试
一、单选题
-
1. 设全集U={ |﹣1<x<5},集合A={1,3},则集合∁UA的子集的个数是( )A、16 B、8 C、7 D、42. 已知复数 在复平面内的对应点关于实轴对称, ( 为虚数单位),则 ( )A、 B、 C、 D、3. 空气质量指数 是一种反映和评价空气质量的方法, 指数与空气质量对应如下表所示:
0~50
51~100
101~150
151~200
201~300
300以上
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某城市2018年12月全月的指 数变化统计图.
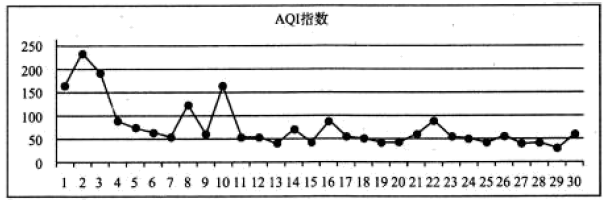
根据统计图判断,下列结论正确的是( )
A、整体上看,这个月的空气质量越来越差 B、整体上看,前半月的空气质量好于后半月的空气质量 C、从 数据看,前半月的方差大于后半月的方差 D、从 数据看,前半月的平均值小于后半月的平均值4. 七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形,现从该正方形中任取一点,则此点取自黑色部分的概率是( ) A、 B、 C、 D、5. 已知 满足 ,则 ( )A、 B、 C、 D、6. 等差数列 中的 是函数 的两个极值点,则 ( )A、5 B、4 C、3 D、27. 若某几何体的三视图如图所示,则此几何体的体积等于
A、 B、 C、 D、5. 已知 满足 ,则 ( )A、 B、 C、 D、6. 等差数列 中的 是函数 的两个极值点,则 ( )A、5 B、4 C、3 D、27. 若某几何体的三视图如图所示,则此几何体的体积等于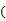
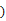
 A、24 B、30 C、10 D、608. 若 是两个非零向量,且 ,则 与 的夹角为( )A、30° B、45° C、60° D、90°9. 的展开式中剔除常数项后的各项系数和为( )A、-55 B、-61 C、-63 D、-7310. 在 中, 分别为内角 的对边,若 , ,且 ,则 ( )A、2 B、3 C、4 D、511. 已知函数 为 内的奇函数,且当 时, ,记 ,则 间的大小关系是( )A、 B、 C、 D、12. 设抛物线 的焦点为 ,过点 的直线与抛物线相交于 , 两点,与抛物线的准线相交于 , ,则 与 的面积之比 ( ).A、 B、 C、 D、
A、24 B、30 C、10 D、608. 若 是两个非零向量,且 ,则 与 的夹角为( )A、30° B、45° C、60° D、90°9. 的展开式中剔除常数项后的各项系数和为( )A、-55 B、-61 C、-63 D、-7310. 在 中, 分别为内角 的对边,若 , ,且 ,则 ( )A、2 B、3 C、4 D、511. 已知函数 为 内的奇函数,且当 时, ,记 ,则 间的大小关系是( )A、 B、 C、 D、12. 设抛物线 的焦点为 ,过点 的直线与抛物线相交于 , 两点,与抛物线的准线相交于 , ,则 与 的面积之比 ( ).A、 B、 C、 D、二、填空题
-
13. 函数 的图象在 处的切线与直线 互相垂直,则 .14. 设变量 满足约束条件 ,则 的最大值是.15. 当双曲线M: 的离心率取得最小值时,双曲线M的渐近线方程为 .16. 已知定义在 上的函数 的图象关于点 对称, ,若函数 图象与函数 图象的交点为 ,则 .
三、解答题
-
17. 设数列 的前 项和为 ,且满足 .(1)、若 为等比数列,求 的值及数列 的通项公式;(2)、在(1)的条件下,设 ,求数列 的前 项和 .18. 从某公司生产线生产的某种产品中抽取1000件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
 (1)、求这1000件产品质量指标的样本平均数 和样本方差 (同一组中的数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标值 服从正态分布 ,其中 近似为样本平均数 近似为样本方差 .
(1)、求这1000件产品质量指标的样本平均数 和样本方差 (同一组中的数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标值 服从正态分布 ,其中 近似为样本平均数 近似为样本方差 .(i)利用该正态分布,求 ;
(ⅱ)已知每件该产品的生产成本为10元,每件合格品(质量指标值 )的定价为16元;若为次品(质量指标值 ),除了全额退款外且每件次品还须赔付客户48元.若该公司卖出100件这种产品,记 表示这件产品的利润,求 .
附: ,若 ,则 .
19. 如图,在侧棱垂直于底面的三棱柱 中, 为侧面 的对角线的交点, 分别为棱 的中点. (1)、求证:平面 //平面 ;(2)、求二面角 的余弦值.20. 已知椭圆 的长轴长为 ,且椭圆 与圆 的公共弦长为(1)、求椭圆 的方程.(2)、过点 作斜率为 的直线 与椭圆 交于两点 ,试判断在 轴上是否存在点 ,使得 为以 为底边的等腰三角形.若存在,求出点 的横坐标的取值范围,若不存在,请说明理由.
(1)、求证:平面 //平面 ;(2)、求二面角 的余弦值.20. 已知椭圆 的长轴长为 ,且椭圆 与圆 的公共弦长为(1)、求椭圆 的方程.(2)、过点 作斜率为 的直线 与椭圆 交于两点 ,试判断在 轴上是否存在点 ,使得 为以 为底边的等腰三角形.若存在,求出点 的横坐标的取值范围,若不存在,请说明理由.